|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГАМИЛЬТОНА - ЯКОБИ ТЕОРИЯЗначение ГАМИЛЬТОНА - ЯКОБИ ТЕОРИЯ в математической энциклопедии: раздел классического вариационного исчисления и аналитич. механики, в к-ром задача нахождения экстремалей (или задача интегрирования гамильтоновой системы уравнений) сводится к интегрированию нек-рого уравнения с частными производными 1-го порядка - так наз. уравнения Гамильтона - Якоби. Основы Г.- Я. т. были разработаны У. Гамильтоном (W. Hamilton) в 20-х гг. 19 в. в применении к задачам волновой и геометрич. оптики. В 1834 У. Гамильтон распространил свои идеи на задачи динамики, а в 1837 К. Якоби (С. Jacobi) применил этот метод для общих задач классического вариационного исчисления. Исходные позиции Г. -Я. <т. были заложены в 17 в. П. Ферма и X. Гюйгенсом на материале геометрич. оптики (см. Ферма принцип и Гюйгенса принцип). Рассмотрим, следуя У. Гамильтону, задачу о распространении света в неоднородной (но для простоты - изотропной) среде, где v(x)-локальная скорость света в точке х. В соответствии с принципом Ферма свет в неоднородной среде распространяется от точки к точке за кратчайшее время. Пусть из к-рого следует уравнение Гамильтона - Якоби для задач геометрич. оптики: В аналитич. механике роль принципа Ферма играет вариационный Гамильтона -Остроградского принцип, а роль эйконала играет функция действия, представляющая собой интеграл вдоль траектории К. Якоби предложил рассматривать функцию действия, подобную (1), для любой задачи классического вариационного исчисления. Экстремали задачи где Последнее соотношение приводит к уравнению для функции S: Это уравнение и наз. уравнением Гамильтон а - Якоби. Важнейшим результатом Г. -Я. т. является теорема Якоби, заключающаяся в том, что полный интеграл уравнения (2), т. е. решение Несмотря на то, что интегрирование уравнений с частными производными составляет, как правило, более сложную задачу, чем отыскание решений обыкновенных уравнений, Г. -Я. т. оказалась мощным орудием исследования задач оптики, механики и геометрии. Суть принципа Гюйгенса была применена Р. Беллманом (R. Bellmann) к задачам оптимального управления. См. также Гильберта, инвариантный интеграл. Лит.:[1] Вариационные принципы механики, М., 1959; [2] Парс Л.-А., Аналитическая динамика, пер. е англ., М., 1971, с. 283-86; [3] Арнольд В. И., Математические методы классической механики, М., 1974, с. 219-24; [4] Ахиезер Н. И., Лекции по вариационному исчислению, М., 1955, с. 92-96. В. М. Тихомиров. |
|
|
|

 исходная точка, а
исходная точка, а  - минимальное время, требуемое свету для преодоления пути от х 0 к х. Функцию
- минимальное время, требуемое свету для преодоления пути от х 0 к х. Функцию  называют эйконалом, или оптической длиной пути. Допустим, что за малое время
называют эйконалом, или оптической длиной пути. Допустим, что за малое время  свет распространился из точки хдо точки
свет распространился из точки хдо точки  . В соответствии с Гюйгенса принципом свет с точностью до малых более высокого порядка будет распространяться по нормали к поверхности уровня функции W(x). Таким образом выполняется равенство
. В соответствии с Гюйгенса принципом свет с точностью до малых более высокого порядка будет распространяться по нормали к поверхности уровня функции W(x). Таким образом выполняется равенство 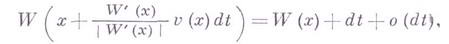


 , соединяющей фиксированную точку
, соединяющей фиксированную точку  с точкой
с точкой  , где L - функция Лагранжа механич. системы.
, где L - функция Лагранжа механич. системы.
 , исходящие из точки
, исходящие из точки 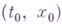 , пересекают поверхность уровня функции действия трансверсально (см. Трансверсальности условие), из этого выводят вид дифференциала функции действия:
, пересекают поверхность уровня функции действия трансверсально (см. Трансверсальности условие), из этого выводят вид дифференциала функции действия:
 - Гамильтона функция (см. также Лежандра преобразование).
- Гамильтона функция (см. также Лежандра преобразование).
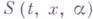 этого уравнения, зависящее от параметров
этого уравнения, зависящее от параметров  (с условием невырожденности
(с условием невырожденности  ), позволяет получить общий интеграл уравнения Эйлера функционала (1), или, что то же самое,- гамильтоновой системы, связанной с этим функционалом, по формулам
), позволяет получить общий интеграл уравнения Эйлера функционала (1), или, что то же самое,- гамильтоновой системы, связанной с этим функционалом, по формулам  Применение теоремы Якоби к интегрированию гамильтоновых систем основано, как правило, на методе разделения переменных в специально выбранных координатах.
Применение теоремы Якоби к интегрированию гамильтоновых систем основано, как правило, на методе разделения переменных в специально выбранных координатах.