"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЭЛЛИПТИЧЕСКАЯ КРИВАЯ
Значение ЭЛЛИПТИЧЕСКАЯ КРИВАЯ в математической энциклопедии:
- неособая полная алгебраическая кривая рода 1. Теория Э. к. является истоком большей части современной алгебраич. геометрии. Но исторически теория Э. к. возникла как часть анализа, как теория эллиптических интегралов и эллиптических функций.
Примеры. Неособая проективная плоская кубич. кривая, пересечение двух неособых квадрик в трехмерном проективном пространстве, двулистное накрытие проективной прямой, разветвленное ровно в четырех точках, а также одномерное абелево многообразие и главное однородное пространство над ним являются Э. к.
Геометрия Э. к. Пусть X - Э. к. над алгебраически замкнутым полем k. Тогда Xбирегулярно изоморфна плоской кубич. кривой (см. [1], [9], [13]). Если  то в проективной плоскости Р 2 существует аффинная система координат, в к-рой Xимеет уравнение в нормальной форме Вейерштрасса
то в проективной плоскости Р 2 существует аффинная система координат, в к-рой Xимеет уравнение в нормальной форме Вейерштрасса

Кривая Xнеособа тогда и только тогда, когда многочлен х 3+ах+b не имеет кратных корней, т. е. дискриминант  В Р 2 кривая (1) имеет единственную точку на бесконечности, к-рую обозначают Р 0; Р0 - точка перегиба кривой (1), а касательная в P0 - бесконечно удаленная прямая, j-инвариант Э. к. X
В Р 2 кривая (1) имеет единственную точку на бесконечности, к-рую обозначают Р 0; Р0 - точка перегиба кривой (1), а касательная в P0 - бесконечно удаленная прямая, j-инвариант Э. к. X

не зависит от выбора системы координат. Равенство j-инвариантов двух Э. к. равносильно тому, что эти Э. к. бирегулярно изоморфны. Для любого  найдется Э. к. Xнад kс j(X)=j.
найдется Э. к. Xнад kс j(X)=j.
Групповая структура на Э. к. Пусть  - фиксированная точка Э. к. X. Отображение
- фиксированная точка Э. к. X. Отображение  сопоставляющее точке
сопоставляющее точке  дивизор Р-Р0 на Э. к. X, устанавливает взаимно однозначное соответствие между Э. к. Xи группой
дивизор Р-Р0 на Э. к. X, устанавливает взаимно однозначное соответствие между Э. к. Xи группой  классов дивизоров степени 0 на X, т. е. Пикара многообразием кривой X. Это соответствие переносит на Xструктуру коммутативной группы, к-рая согласована со структурой алгебраич. многообразия и превращает X в одномерное абелево многообразие (X, Р0); точка Р 0 при этом является нулем группы. Введенная групповая структура допускает следующее геометрич. описание. Пусть
классов дивизоров степени 0 на X, т. е. Пикара многообразием кривой X. Это соответствие переносит на Xструктуру коммутативной группы, к-рая согласована со структурой алгебраич. многообразия и превращает X в одномерное абелево многообразие (X, Р0); точка Р 0 при этом является нулем группы. Введенная групповая структура допускает следующее геометрич. описание. Пусть  - плоская кубич. кривая. Тогда сумма точек Ри Qопределяется правилом
- плоская кубич. кривая. Тогда сумма точек Ри Qопределяется правилом  где
где  - третья точка пересечения кривой Xс прямой, проходящей через точки Ри Q. Иначе говоря, сумма трех точек на Xравна нулю тогда и только тогда, когда они лежат на одном прямой.
- третья точка пересечения кривой Xс прямой, проходящей через точки Ри Q. Иначе говоря, сумма трех точек на Xравна нулю тогда и только тогда, когда они лежат на одном прямой.
Э. к. как одномерное абелево многообразие. Пусть п X обозначает эндоморфизм умножения на  в (X, Р 0). Если (Y, Q0) - Э. к. с отмеченной точкой Q0,то любое рациональное отображение
в (X, Р 0). Если (Y, Q0) - Э. к. с отмеченной точкой Q0,то любое рациональное отображение  имеет вид f(P) = h(P)+Q1, где
имеет вид f(P) = h(P)+Q1, где 
 - гомоморфизм абелевых многообразий. При этом гомоморфизм hявляется либо постоянным отображением в точку Q0, либо изогенией, т. е. существует гомоморфизм абелевых многообразий
- гомоморфизм абелевых многообразий. При этом гомоморфизм hявляется либо постоянным отображением в точку Q0, либо изогенией, т. е. существует гомоморфизм абелевых многообразий  такой, что
такой, что  для нек-рого п(см. [1], [6]).
для нек-рого п(см. [1], [6]).
Группа автоморфизмов Э. к. А* действует транзитивно на А. а ее подгруппа G=Aut(X, P0) автоморфизмов, оставляющих на месте точку Р 0, нетривиальна и конечна. Пусть char kотлична от 2 и 3. Если j(X)не равно 0 или 1728, то группа Gсостоит из двух элементов 1X и (- )X. Порядок Gравен 4 при j(X) =1728 и 6 при j(X)=0 (см. [1], [6], [13]).
Важным инвариантом Э. к. является кольцо эндоморфизмов R=End(X, P0) абелева многообразия (X, Р 0). Отображение  определяет вложение
определяет вложение  Если
Если  то говорят, что X - Э. к. с комплексным умножением. Кольцо R может быть одного из следующих типов (см. [1], [9], [13]): I.
то говорят, что X - Э. к. с комплексным умножением. Кольцо R может быть одного из следующих типов (см. [1], [9], [13]): I. 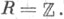 II.
II.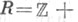
 Здесь
Здесь  -кольцо целых алгебраич. чисел мнимого квадратичного поля
-кольцо целых алгебраич. чисел мнимого квадратичного поля 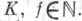 III. R - некоммутативная
III. R - некоммутативная 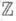 -алгебра ранга 4 без делителей нуля. В этом случае р=char k>0 и R- порядок в алгeбре кватернионов над
-алгебра ранга 4 без делителей нуля. В этом случае р=char k>0 и R- порядок в алгeбре кватернионов над  разветвленной только в р и
разветвленной только в р и  Такие Э. к. существуют для всех ри наз. сулерсингулярными; несунерсингулярные Э. к. в характеристике р наз. обыкновенными Э. к.
Такие Э. к. существуют для всех ри наз. сулерсингулярными; несунерсингулярные Э. к. в характеристике р наз. обыкновенными Э. к.
Группа Х n= Кеr п X точек Э. к. X, порядок к-рых делит п, имеет следующую структуру:  если (n, char k) = 1. При р = char k > 0 для обыкновенных Э. к.
если (n, char k) = 1. При р = char k > 0 для обыкновенных Э. к.  а для суперсингулярных Э. к.
а для суперсингулярных Э. к.  Для простого
Для простого  Тейта модуль Tl(X)изоморфен
Тейта модуль Tl(X)изоморфен 
Э. к. над незамкнутыми полями. Пусть X - Э. к. над произвольным полем k. Если множество k-рациональных точек X(k)кривой Xнепусто, то Xбирегулярно изоморфна плоской кубич. кривой (1) с  3). Бесконечно удаленная точка P0 кривой (1) определена над k. Как и выше, можно определить групповую структуру на кривой (1), превращающую Xв одномерное абелево многообразие над k, а множество X(k)в коммутативную группу с нулем P0. Если kконечно порождено над своим простым под-полем, то X(k) - группа с конечным числом образующих (теорема Морделла - Вейля).
3). Бесконечно удаленная точка P0 кривой (1) определена над k. Как и выше, можно определить групповую структуру на кривой (1), превращающую Xв одномерное абелево многообразие над k, а множество X(k)в коммутативную группу с нулем P0. Если kконечно порождено над своим простым под-полем, то X(k) - группа с конечным числом образующих (теорема Морделла - Вейля).
Для любой Э. к. Xопределено Якоби многообразие J(X), являющееся одномерным абелевым многообразием над k. Э. к. Xявляется главным однородным пространством над J(X). Если множество X(k)непусто, то выбор точки  задает изоморфизм X~J(X), при к-ром точка Р 0 переходит в нуль группы J(X). В общем случае Э. к. Xи J(X)изоморфны над конечным расширением поля k(см. [1], [4), [13]).
задает изоморфизм X~J(X), при к-ром точка Р 0 переходит в нуль группы J(X). В общем случае Э. к. Xи J(X)изоморфны над конечным расширением поля k(см. [1], [4), [13]).
Э. к. над полем комплексных чисел. Э. к. Xнад  является компактной римановой поверхностью рода 1 и обратно. Групповая структура превращает Xв комплексную группу Ли, являющуюся одномерным комплексным тором
является компактной римановой поверхностью рода 1 и обратно. Групповая структура превращает Xв комплексную группу Ли, являющуюся одномерным комплексным тором  где
где  -решетка в комплексной плоскости
-решетка в комплексной плоскости  Обратно, любой одномерный комплексный тор является Э. к. (см. [3]). С топологич. точки зрения Э. к.- двумерный тор.
Обратно, любой одномерный комплексный тор является Э. к. (см. [3]). С топологич. точки зрения Э. к.- двумерный тор.
Теория Э. к. над полем  по существу, эквивалентна теории эллиптич. функций. Отождествление тора
по существу, эквивалентна теории эллиптич. функций. Отождествление тора  с Э. к. осуществляется следующим образом. Эллиптич. функции с данной решеткой периодов L образуют поле, порожденное
с Э. к. осуществляется следующим образом. Эллиптич. функции с данной решеткой периодов L образуют поле, порожденное  -функцией Вейерштрасса (см. Вейерштрасса эллиптические функции )и ее производной
-функцией Вейерштрасса (см. Вейерштрасса эллиптические функции )и ее производной  к-рые связаны соотношением
к-рые связаны соотношением 
Отображение  индуцирует изоморфизм тора
индуцирует изоморфизм тора  и Э. к.
и Э. к.  с уравнением у 2=4x3-g2x-g3. Отождествление Э. <к. X, заданной уравнением (1), с тором
с уравнением у 2=4x3-g2x-g3. Отождествление Э. <к. X, заданной уравнением (1), с тором  осуществляется с помощью криволинейных интегралов от голоморфной формы
осуществляется с помощью криволинейных интегралов от голоморфной формы 
 и приводит к совпадению Э. <к. X с ее многообразием Якоби J(X).
и приводит к совпадению Э. <к. X с ее многообразием Якоби J(X).
Описание множества всех Э. <к. как торов 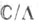 приводит к модулярной функции
приводит к модулярной функции  Две решетки
Две решетки  и
и  определяют изоморфные торы тогда и только тогда, когда они подобны, т: е. одна получается из другой умножением на комплексное число. Поэтому можно считать, что решетка
определяют изоморфные торы тогда и только тогда, когда они подобны, т: е. одна получается из другой умножением на комплексное число. Поэтому можно считать, что решетка  порождена числами 1 и
порождена числами 1 и  из
из 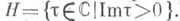 Две решетки с базисами 1,
Две решетки с базисами 1,  и 1,
и 1,  подобны тогда н только тогда, когда
подобны тогда н только тогда, когда  для нек-рого элемента модулярной группы Г. Модулярная функция
для нек-рого элемента модулярной группы Г. Модулярная функция


наз. также абсолютным инвариантом;  тогда и только тогда, когда
тогда и только тогда, когда  для нек-рого
для нек-рого  и функция
и функция  осуществляет взаимно однозначное соответствие между классами изоморфных Э. к. над С и комплексными числами. Если
осуществляет взаимно однозначное соответствие между классами изоморфных Э. к. над С и комплексными числами. Если  то
то 
Э. к. Xесть Э. к. с комплексным умножением тогда и только тогда, когда  - мнимая квадратическая иррациональность. В этом случае R - подкольцо конечного индекса в кольце целых алгебраич. чисел мнимого квадратичного поля
- мнимая квадратическая иррациональность. В этом случае R - подкольцо конечного индекса в кольце целых алгебраич. чисел мнимого квадратичного поля  Э. к. с комплексным умножением тесно связаны с полей классов теорией для мнимых квадратичных полей (см. [4], [8]).
Э. к. с комплексным умножением тесно связаны с полей классов теорией для мнимых квадратичных полей (см. [4], [8]).
Арифметика Э. к. Пусть X- Э. к. над конечным полем kиз qэлементов. Множество X(k)всегда непусто и конечно. Тем самым Xснабжается структурой одномерного абелева многообразия над k, а X(k) - структурой конечной коммутативной группы. Порядок Агруппы Х(k)удовлетворяет неравенству 
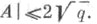 Многочлен t2-(q+1-A)t+q есть характеристич. многочлен Фробениуса эндоморфизма, действующего на модуле Тейта
Многочлен t2-(q+1-A)t+q есть характеристич. многочлен Фробениуса эндоморфизма, действующего на модуле Тейта  Его корни
Его корни  - комплексно сопряженные целые алгебраич. числа, по модулю равные
- комплексно сопряженные целые алгебраич. числа, по модулю равные  Для любого конечного расширения kn поля kстепени ппорядок группы X(kn )равен
Для любого конечного расширения kn поля kстепени ппорядок группы X(kn )равен  Дзета-функция Э. к. Xравна
Дзета-функция Э. к. Xравна

Для любого целого алгебраического  лежащего в нек-ром мнимом квадратичном поле (или в
лежащего в нек-ром мнимом квадратичном поле (или в  и по модулю равного
и по модулю равного  найдется такая Э. к. X над k, что порядок группы X(k) равен
найдется такая Э. к. X над k, что порядок группы X(k) равен 
Пусть k - поле p-адических чисел  или его конечное алгебраич. расширение, В - кольцо целых поля k, X - Э. к. над k и пусть множество X(k)непусто. Групповая структура превращает X(k)в коммутативную компактную одномерную Ли р-адическую группу. Группа X(k)двойственна по Понтрягину к Вейля- Шатле группе WC(k, X). Если
или его конечное алгебраич. расширение, В - кольцо целых поля k, X - Э. к. над k и пусть множество X(k)непусто. Групповая структура превращает X(k)в коммутативную компактную одномерную Ли р-адическую группу. Группа X(k)двойственна по Понтрягину к Вейля- Шатле группе WC(k, X). Если  то X -кривая Тейта (см. [1], 15]) и существует канонич. униформизация группы X(k), аналогичная случаю поля
то X -кривая Тейта (см. [1], 15]) и существует канонич. униформизация группы X(k), аналогичная случаю поля 
Пусть X - Э. к. над  и множество
и множество  непусто. Тогда А бирегулярно изоморфна кривой (1) с
непусто. Тогда А бирегулярно изоморфна кривой (1) с  Из всех кривых вида (1) с целыми аи b, изоморфных X, выбирается такая, для к-рой абсолютная величина дискриминанта
Из всех кривых вида (1) с целыми аи b, изоморфных X, выбирается такая, для к-рой абсолютная величина дискриминанта  минимальна. Кондуктор N и L- функция L(X, s) Э. к. X определяются как формальные произведения локальных множителей
минимальна. Кондуктор N и L- функция L(X, s) Э. к. X определяются как формальные произведения локальных множителей

по всем простым р(см. [1], [5], [13]). Здесь fp- нек-рая степень р, Lp(X, s) - мероморфная функция комплексного переменного s, не имеющая ни нуля, ни полюса при s=l. Чтобы определить локальные множители, рассматривается редукция кривой Х по модулю  - плоская проективная кривая X р над полем вычетов
- плоская проективная кривая X р над полем вычетов  заданная в аффинной системе координат уравнением
заданная в аффинной системе координат уравнением
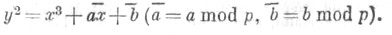
Пусть А р - число  -точек на Х р. Если рне делит
-точек на Х р. Если рне делит  то Х р - Э. к. <над
то Х р - Э. к. <над  и полагают
и полагают

Если рделит  то многочлен
то многочлен  имеет кратный корень и полагают
имеет кратный корень и полагают

(в зависимости от того, является этот корень трехкратным или нет). Произведение (2) сходится в правой полуплоскости  Предполагается, что L(X,s )мероморфно продолжается на всю комплексную плоскость и что функция
Предполагается, что L(X,s )мероморфно продолжается на всю комплексную плоскость и что функция

(Г(s) -гамма-функция )удовлетворяет функциональному уравнению  с
с  (см. [5], [13]). Эта гипотеза доказана для Э. к. с комплексным умножением.
(см. [5], [13]). Эта гипотеза доказана для Э. к. с комплексным умножением.
Группа  изоморфна
изоморфна  где
где  -конечная абелева группа, a F - свободная абелева. группа нек-рого конечного ранга r. Группа
-конечная абелева группа, a F - свободная абелева. группа нек-рого конечного ранга r. Группа  изоморфна одной из следующих 15 групп (см. [11]):
изоморфна одной из следующих 15 групп (см. [11]):
 или т=12 и
или т=12 и  Число rназ. рангом Э. к. над
Число rназ. рангом Э. к. над  или
или  -рангом. Известны примеры Э. к. над
-рангом. Известны примеры Э. к. над  ранга
ранга 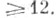 Имеется предположение (см. [1], [13]), что над Qсуществуют Э. к. сколь угодно большого ранга.
Имеется предположение (см. [1], [13]), что над Qсуществуют Э. к. сколь угодно большого ранга.
Для изучения группы  используется высота Тейта
используется высота Тейта  являющаяся неотрицательно определенной квадратичной формой на
являющаяся неотрицательно определенной квадратичной формой на  (см. [1], [3], [8], а также Высота в диофантовой геометрии). Для любого
(см. [1], [3], [8], а также Высота в диофантовой геометрии). Для любого  множество
множество 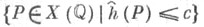 конечно. В частности,
конечно. В частности,  обращается в 0 в точности на подгруппе кручения
обращается в 0 в точности на подгруппе кручения 
Важным инвариантом Э. к. Xявляется ее группа Тейта - Шафаревича Ш (X)(см. Вейля- Шатле группа). Нетривиальные элементы группы Ш(Х) - Э. к., не имеющие  -точек,- доставляют примеры Э. к., для к-рых не выполнен Хассе принцип. Группа Ш(Х) периодична и для любого пподгруппа ее элементов, порядки к-рых делят и, конечна. Для большого числа Э. к. проверена конечность 2- и 3-компонент группы Ш (см. [1], [4], [5]). Имеется гипотеза, что и группа Ш конечна.
-точек,- доставляют примеры Э. к., для к-рых не выполнен Хассе принцип. Группа Ш(Х) периодична и для любого пподгруппа ее элементов, порядки к-рых делят и, конечна. Для большого числа Э. к. проверена конечность 2- и 3-компонент группы Ш (см. [1], [4], [5]). Имеется гипотеза, что и группа Ш конечна.
Гипотеза Берча и Суиннертон-Дайера (см. [5], [13]) утверждает, что порядок нуля L-функции L(X, s )при s=l равен  -рангу Э. к. X. В частности, L(X, s )имеет нуль при s=1 тогда и только тогда, когда группа
-рангу Э. к. X. В частности, L(X, s )имеет нуль при s=1 тогда и только тогда, когда группа  бесконечна. Гипотеза не доказана ни для одной Э. к. (1984), хотя для Э. к. с комплексным умножением (и f=1) установлено, что бесконечность
бесконечна. Гипотеза не доказана ни для одной Э. к. (1984), хотя для Э. к. с комплексным умножением (и f=1) установлено, что бесконечность  влечет за собой наличие нуля у L-функция при s=1 (см. [14]). Гипотеза Берча и Суиннертон-Дайера дает главный член асимптотики L-функции при
влечет за собой наличие нуля у L-функция при s=1 (см. [14]). Гипотеза Берча и Суиннертон-Дайера дает главный член асимптотики L-функции при  в к-рый входят порядки групп Ш(X)и
в к-рый входят порядки групп Ш(X)и  определитель высоты Тейта [1]. Эта гипотеза допускает переформулировку в терминах Тамагавы чисел (см. [7]).
определитель высоты Тейта [1]. Эта гипотеза допускает переформулировку в терминах Тамагавы чисел (см. [7]).
Предполагается (гипотеза Вейля), что существует униформизация Э. к. Xмодулярными функциями относительно конгруэнц-подгрунпы Г 0(N)модулярной группы Г (см. [5], а также Дзета-функция в алгебраич. геометрии). Эта гипотеза доказана для Э. к. с комплексным умножением. Известно (см. [15]), что всякая алгебраич. кривая над  униформизуется модулярными функциями относительно нек-рой подгруппы конечного индекса группы Г.
униформизуется модулярными функциями относительно нек-рой подгруппы конечного индекса группы Г.
Лит.:[1] Касселс Дж., лМатематика

 то в проективной плоскости Р 2 существует аффинная система координат, в к-рой Xимеет уравнение в нормальной форме Вейерштрасса
то в проективной плоскости Р 2 существует аффинная система координат, в к-рой Xимеет уравнение в нормальной форме Вейерштрасса 
 В Р 2 кривая (1) имеет единственную точку на бесконечности, к-рую обозначают Р 0; Р0 - точка перегиба кривой (1), а касательная в P0 - бесконечно удаленная прямая, j-инвариант Э. к. X
В Р 2 кривая (1) имеет единственную точку на бесконечности, к-рую обозначают Р 0; Р0 - точка перегиба кривой (1), а касательная в P0 - бесконечно удаленная прямая, j-инвариант Э. к. X 
 найдется Э. к. Xнад kс j(X)=j.
найдется Э. к. Xнад kс j(X)=j.  - фиксированная точка Э. к. X. Отображение
- фиксированная точка Э. к. X. Отображение  сопоставляющее точке
сопоставляющее точке  дивизор Р-Р0 на Э. к. X, устанавливает взаимно однозначное соответствие между Э. к. Xи группой
дивизор Р-Р0 на Э. к. X, устанавливает взаимно однозначное соответствие между Э. к. Xи группой  классов дивизоров степени 0 на X, т. е. Пикара многообразием кривой X. Это соответствие переносит на Xструктуру коммутативной группы, к-рая согласована со структурой алгебраич. многообразия и превращает X в одномерное абелево многообразие (X, Р0); точка Р 0 при этом является нулем группы. Введенная групповая структура допускает следующее геометрич. описание. Пусть
классов дивизоров степени 0 на X, т. е. Пикара многообразием кривой X. Это соответствие переносит на Xструктуру коммутативной группы, к-рая согласована со структурой алгебраич. многообразия и превращает X в одномерное абелево многообразие (X, Р0); точка Р 0 при этом является нулем группы. Введенная групповая структура допускает следующее геометрич. описание. Пусть  - плоская кубич. кривая. Тогда сумма точек Ри Qопределяется правилом
- плоская кубич. кривая. Тогда сумма точек Ри Qопределяется правилом  где
где  - третья точка пересечения кривой Xс прямой, проходящей через точки Ри Q. Иначе говоря, сумма трех точек на Xравна нулю тогда и только тогда, когда они лежат на одном прямой.
- третья точка пересечения кривой Xс прямой, проходящей через точки Ри Q. Иначе говоря, сумма трех точек на Xравна нулю тогда и только тогда, когда они лежат на одном прямой.  в (X, Р 0). Если (Y, Q0) - Э. к. с отмеченной точкой Q0,то любое рациональное отображение
в (X, Р 0). Если (Y, Q0) - Э. к. с отмеченной точкой Q0,то любое рациональное отображение  имеет вид f(P) = h(P)+Q1, где
имеет вид f(P) = h(P)+Q1, где 
 - гомоморфизм абелевых многообразий. При этом гомоморфизм hявляется либо постоянным отображением в точку Q0, либо изогенией, т. е. существует гомоморфизм абелевых многообразий
- гомоморфизм абелевых многообразий. При этом гомоморфизм hявляется либо постоянным отображением в точку Q0, либо изогенией, т. е. существует гомоморфизм абелевых многообразий  такой, что
такой, что  для нек-рого п(см. [1], [6]).
для нек-рого п(см. [1], [6]).  определяет вложение
определяет вложение  Если
Если  то говорят, что X - Э. к. с комплексным умножением. Кольцо R может быть одного из следующих типов (см. [1], [9], [13]): I.
то говорят, что X - Э. к. с комплексным умножением. Кольцо R может быть одного из следующих типов (см. [1], [9], [13]): I. 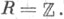 II.
II.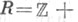
 Здесь
Здесь  -кольцо целых алгебраич. чисел мнимого квадратичного поля
-кольцо целых алгебраич. чисел мнимого квадратичного поля 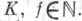 III. R - некоммутативная
III. R - некоммутативная 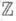 -алгебра ранга 4 без делителей нуля. В этом случае р=char k>0 и R- порядок в алгeбре кватернионов над
-алгебра ранга 4 без делителей нуля. В этом случае р=char k>0 и R- порядок в алгeбре кватернионов над  разветвленной только в р и
разветвленной только в р и  Такие Э. к. существуют для всех ри наз. сулерсингулярными; несунерсингулярные Э. к. в характеристике р наз. обыкновенными Э. к.
Такие Э. к. существуют для всех ри наз. сулерсингулярными; несунерсингулярные Э. к. в характеристике р наз. обыкновенными Э. к.  если (n, char k) = 1. При р = char k > 0 для обыкновенных Э. к.
если (n, char k) = 1. При р = char k > 0 для обыкновенных Э. к.  а для суперсингулярных Э. к.
а для суперсингулярных Э. к.  Для простого
Для простого  Тейта модуль Tl(X)изоморфен
Тейта модуль Tl(X)изоморфен 
 3). Бесконечно удаленная точка P0 кривой (1) определена над k. Как и выше, можно определить групповую структуру на кривой (1), превращающую Xв одномерное абелево многообразие над k, а множество X(k)в коммутативную группу с нулем P0. Если kконечно порождено над своим простым под-полем, то X(k) - группа с конечным числом образующих (теорема Морделла - Вейля).
3). Бесконечно удаленная точка P0 кривой (1) определена над k. Как и выше, можно определить групповую структуру на кривой (1), превращающую Xв одномерное абелево многообразие над k, а множество X(k)в коммутативную группу с нулем P0. Если kконечно порождено над своим простым под-полем, то X(k) - группа с конечным числом образующих (теорема Морделла - Вейля).  задает изоморфизм X~J(X), при к-ром точка Р 0 переходит в нуль группы J(X). В общем случае Э. к. Xи J(X)изоморфны над конечным расширением поля k(см. [1], [4), [13]).
задает изоморфизм X~J(X), при к-ром точка Р 0 переходит в нуль группы J(X). В общем случае Э. к. Xи J(X)изоморфны над конечным расширением поля k(см. [1], [4), [13]).  является компактной римановой поверхностью рода 1 и обратно. Групповая структура превращает Xв комплексную группу Ли, являющуюся одномерным комплексным тором
является компактной римановой поверхностью рода 1 и обратно. Групповая структура превращает Xв комплексную группу Ли, являющуюся одномерным комплексным тором  где
где  -решетка в комплексной плоскости
-решетка в комплексной плоскости  Обратно, любой одномерный комплексный тор является Э. к. (см. [3]). С топологич. точки зрения Э. к.- двумерный тор.
Обратно, любой одномерный комплексный тор является Э. к. (см. [3]). С топологич. точки зрения Э. к.- двумерный тор.  по существу, эквивалентна теории эллиптич. функций. Отождествление тора
по существу, эквивалентна теории эллиптич. функций. Отождествление тора  с Э. к. осуществляется следующим образом. Эллиптич. функции с данной решеткой периодов L образуют поле, порожденное
с Э. к. осуществляется следующим образом. Эллиптич. функции с данной решеткой периодов L образуют поле, порожденное  -функцией Вейерштрасса (см. Вейерштрасса эллиптические функции )и ее производной
-функцией Вейерштрасса (см. Вейерштрасса эллиптические функции )и ее производной  к-рые связаны соотношением
к-рые связаны соотношением 
 индуцирует изоморфизм тора
индуцирует изоморфизм тора  и Э. к.
и Э. к.  с уравнением у 2=4x3-g2x-g3. Отождествление Э. <к. X, заданной уравнением (1), с тором
с уравнением у 2=4x3-g2x-g3. Отождествление Э. <к. X, заданной уравнением (1), с тором  осуществляется с помощью криволинейных интегралов от голоморфной формы
осуществляется с помощью криволинейных интегралов от голоморфной формы 
 и приводит к совпадению Э. <к. X с ее многообразием Якоби J(X).
и приводит к совпадению Э. <к. X с ее многообразием Якоби J(X). 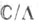 приводит к модулярной функции
приводит к модулярной функции  Две решетки
Две решетки  и
и  определяют изоморфные торы тогда и только тогда, когда они подобны, т: е. одна получается из другой умножением на комплексное число. Поэтому можно считать, что решетка
определяют изоморфные торы тогда и только тогда, когда они подобны, т: е. одна получается из другой умножением на комплексное число. Поэтому можно считать, что решетка  порождена числами 1 и
порождена числами 1 и  из
из 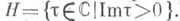 Две решетки с базисами 1,
Две решетки с базисами 1,  и 1,
и 1,  подобны тогда н только тогда, когда
подобны тогда н только тогда, когда  для нек-рого элемента модулярной группы Г. Модулярная функция
для нек-рого элемента модулярной группы Г. Модулярная функция 

 тогда и только тогда, когда
тогда и только тогда, когда  для нек-рого
для нек-рого  и функция
и функция  осуществляет взаимно однозначное соответствие между классами изоморфных Э. к. над С и комплексными числами. Если
осуществляет взаимно однозначное соответствие между классами изоморфных Э. к. над С и комплексными числами. Если  то
то 
 - мнимая квадратическая иррациональность. В этом случае R - подкольцо конечного индекса в кольце целых алгебраич. чисел мнимого квадратичного поля
- мнимая квадратическая иррациональность. В этом случае R - подкольцо конечного индекса в кольце целых алгебраич. чисел мнимого квадратичного поля  Э. к. с комплексным умножением тесно связаны с полей классов теорией для мнимых квадратичных полей (см. [4], [8]).
Э. к. с комплексным умножением тесно связаны с полей классов теорией для мнимых квадратичных полей (см. [4], [8]). 
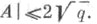 Многочлен t2-(q+1-A)t+q есть характеристич. многочлен Фробениуса эндоморфизма, действующего на модуле Тейта
Многочлен t2-(q+1-A)t+q есть характеристич. многочлен Фробениуса эндоморфизма, действующего на модуле Тейта  Его корни
Его корни  - комплексно сопряженные целые алгебраич. числа, по модулю равные
- комплексно сопряженные целые алгебраич. числа, по модулю равные  Для любого конечного расширения kn поля kстепени ппорядок группы X(kn )равен
Для любого конечного расширения kn поля kстепени ппорядок группы X(kn )равен  Дзета-функция Э. к. Xравна
Дзета-функция Э. к. Xравна 
 лежащего в нек-ром мнимом квадратичном поле (или в
лежащего в нек-ром мнимом квадратичном поле (или в  и по модулю равного
и по модулю равного  найдется такая Э. к. X над k, что порядок группы X(k) равен
найдется такая Э. к. X над k, что порядок группы X(k) равен 
 или его конечное алгебраич. расширение, В - кольцо целых поля k, X - Э. к. над k и пусть множество X(k)непусто. Групповая структура превращает X(k)в коммутативную компактную одномерную Ли р-адическую группу. Группа X(k)двойственна по Понтрягину к Вейля- Шатле группе WC(k, X). Если
или его конечное алгебраич. расширение, В - кольцо целых поля k, X - Э. к. над k и пусть множество X(k)непусто. Групповая структура превращает X(k)в коммутативную компактную одномерную Ли р-адическую группу. Группа X(k)двойственна по Понтрягину к Вейля- Шатле группе WC(k, X). Если  то X -кривая Тейта (см. [1], 15]) и существует канонич. униформизация группы X(k), аналогичная случаю поля
то X -кривая Тейта (см. [1], 15]) и существует канонич. униформизация группы X(k), аналогичная случаю поля 
 и множество
и множество  непусто. Тогда А бирегулярно изоморфна кривой (1) с
непусто. Тогда А бирегулярно изоморфна кривой (1) с  Из всех кривых вида (1) с целыми аи b, изоморфных X, выбирается такая, для к-рой абсолютная величина дискриминанта
Из всех кривых вида (1) с целыми аи b, изоморфных X, выбирается такая, для к-рой абсолютная величина дискриминанта  минимальна. Кондуктор N и L- функция L(X, s) Э. к. X определяются как формальные произведения локальных множителей
минимальна. Кондуктор N и L- функция L(X, s) Э. к. X определяются как формальные произведения локальных множителей 
 - плоская проективная кривая X р над полем вычетов
- плоская проективная кривая X р над полем вычетов  заданная в аффинной системе координат уравнением
заданная в аффинной системе координат уравнением 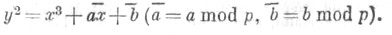
 -точек на Х р. Если рне делит
-точек на Х р. Если рне делит  то Х р - Э. к. <над
то Х р - Э. к. <над  и полагают
и полагают 
 то многочлен
то многочлен  имеет кратный корень и полагают
имеет кратный корень и полагают 
 Предполагается, что L(X,s )мероморфно продолжается на всю комплексную плоскость и что функция
Предполагается, что L(X,s )мероморфно продолжается на всю комплексную плоскость и что функция 
 с
с  (см. [5], [13]). Эта гипотеза доказана для Э. к. с комплексным умножением.
(см. [5], [13]). Эта гипотеза доказана для Э. к. с комплексным умножением.  изоморфна
изоморфна  где
где  -конечная абелева группа, a F - свободная абелева. группа нек-рого конечного ранга r. Группа
-конечная абелева группа, a F - свободная абелева. группа нек-рого конечного ранга r. Группа  изоморфна одной из следующих 15 групп (см. [11]):
изоморфна одной из следующих 15 групп (см. [11]):
 или т=12 и
или т=12 и  Число rназ. рангом Э. к. над
Число rназ. рангом Э. к. над  или
или  -рангом. Известны примеры Э. к. над
-рангом. Известны примеры Э. к. над  ранга
ранга 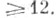 Имеется предположение (см. [1], [13]), что над Qсуществуют Э. к. сколь угодно большого ранга.
Имеется предположение (см. [1], [13]), что над Qсуществуют Э. к. сколь угодно большого ранга.  используется высота Тейта
используется высота Тейта  являющаяся неотрицательно определенной квадратичной формой на
являющаяся неотрицательно определенной квадратичной формой на  (см. [1], [3], [8], а также Высота в диофантовой геометрии). Для любого
(см. [1], [3], [8], а также Высота в диофантовой геометрии). Для любого  множество
множество 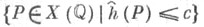 конечно. В частности,
конечно. В частности,  обращается в 0 в точности на подгруппе кручения
обращается в 0 в точности на подгруппе кручения 
 -точек,- доставляют примеры Э. к., для к-рых не выполнен Хассе принцип. Группа Ш(Х) периодична и для любого пподгруппа ее элементов, порядки к-рых делят и, конечна. Для большого числа Э. к. проверена конечность 2- и 3-компонент группы Ш (см. [1], [4], [5]). Имеется гипотеза, что и группа Ш конечна.
-точек,- доставляют примеры Э. к., для к-рых не выполнен Хассе принцип. Группа Ш(Х) периодична и для любого пподгруппа ее элементов, порядки к-рых делят и, конечна. Для большого числа Э. к. проверена конечность 2- и 3-компонент группы Ш (см. [1], [4], [5]). Имеется гипотеза, что и группа Ш конечна.  -рангу Э. к. X. В частности, L(X, s )имеет нуль при s=1 тогда и только тогда, когда группа
-рангу Э. к. X. В частности, L(X, s )имеет нуль при s=1 тогда и только тогда, когда группа  бесконечна. Гипотеза не доказана ни для одной Э. к. (1984), хотя для Э. к. с комплексным умножением (и f=1) установлено, что бесконечность
бесконечна. Гипотеза не доказана ни для одной Э. к. (1984), хотя для Э. к. с комплексным умножением (и f=1) установлено, что бесконечность  влечет за собой наличие нуля у L-функция при s=1 (см. [14]). Гипотеза Берча и Суиннертон-Дайера дает главный член асимптотики L-функции при
влечет за собой наличие нуля у L-функция при s=1 (см. [14]). Гипотеза Берча и Суиннертон-Дайера дает главный член асимптотики L-функции при  в к-рый входят порядки групп Ш(X)и
в к-рый входят порядки групп Ш(X)и  определитель высоты Тейта [1]. Эта гипотеза допускает переформулировку в терминах Тамагавы чисел (см. [7]).
определитель высоты Тейта [1]. Эта гипотеза допускает переформулировку в терминах Тамагавы чисел (см. [7]).  униформизуется модулярными функциями относительно нек-рой подгруппы конечного индекса группы Г.
униформизуется модулярными функциями относительно нек-рой подгруппы конечного индекса группы Г.