"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АЛГЕБРАИЧЕСКАЯ КРИВАЯ
Значение АЛГЕБРАИЧЕСКАЯ КРИВАЯ в математической энциклопедии:
алгебраическое многообразие размерности 1. А. к. является наиболее изученным объектом алгебраической геометрии. В дальнейшем под А. к. понимается, как правило, неприводимая А. к. над алгебраически замкнутым полем.
Наиболее простым и интуитивно ясным является понятие плоской аффинной А. к. Это - множество точек аффинной плоскости  удовлетворяющих уравнению
удовлетворяющих уравнению 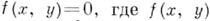 - многочлен с коэффициентами из алгебраически замкнутого поля k. Поле рациональных функций неприводимой А. к. над kесть поле алгебраич. функций одного переменного и имеет вид
- многочлен с коэффициентами из алгебраически замкнутого поля k. Поле рациональных функций неприводимой А. к. над kесть поле алгебраич. функций одного переменного и имеет вид  где хи усвязаны уравнением
где хи усвязаны уравнением 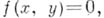 а
а 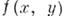 - многочлен над k. Это означает, что всякая А. к. бирационально изоморфна плоской аффинной кривой.
- многочлен над k. Это означает, что всякая А. к. бирационально изоморфна плоской аффинной кривой.
Уже давно было замечено, что даже при изучении аффинных кривых глубокие закономерности удается вскрыть только при учете бесконечно удаленных точек и детальном исследовании особенностей. Для изучения всех точек аффинной кривой ее погружают в проективное пространство  с последующим замыканием в Зариского топологии. Таким образом получается проективная кривая X, причем исходная аффинная кривая У может быть получена из Xвыбрасыванием конечного числа точек. Если Yнеприводима, то Xи Y бирационально изоморфны. Каждая полная А. к. является проективной. Если X - гладкая проективная кривая (г. п. к.), то все кольца нормирования поля
с последующим замыканием в Зариского топологии. Таким образом получается проективная кривая X, причем исходная аффинная кривая У может быть получена из Xвыбрасыванием конечного числа точек. Если Yнеприводима, то Xи Y бирационально изоморфны. Каждая полная А. к. является проективной. Если X - гладкая проективная кривая (г. п. к.), то все кольца нормирования поля 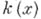 исчерпываются локальными кольцами
исчерпываются локальными кольцами Если две г. п. к. бирационально эквивалентны, то они изоморфны. Нормальная А. к. является гладкой. В частности, всякая неприводимая А. к. бирационально эквивалентна г. п. к. Получаемая в процессе нормализации гладкая проективная модель А. к. лежит в нек-ром пространстве
Если две г. п. к. бирационально эквивалентны, то они изоморфны. Нормальная А. к. является гладкой. В частности, всякая неприводимая А. к. бирационально эквивалентна г. п. к. Получаемая в процессе нормализации гладкая проективная модель А. к. лежит в нек-ром пространстве  Любая г. п. к. изоморфна кривой, расположенной в
Любая г. п. к. изоморфна кривой, расположенной в  Каждая плоская А. к. кремоновым преобразованием может быть преобразована в кривую с обыкновенными особыми точками.
Каждая плоская А. к. кремоновым преобразованием может быть преобразована в кривую с обыкновенными особыми точками.
Дивизоры, на гладкой А. к. представляют собой линейные комбинации точек с целыми коэффициентами

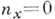 почти для всех х. Если все
почти для всех х. Если все  то дивизор Dназ. положительным, или эффективным, что обозначается
то дивизор Dназ. положительным, или эффективным, что обозначается  Степенью дивизора D наз. число
Степенью дивизора D наз. число

Главные дивизоры образуют подгруппу Р(X).группы Div Xвсех дивизоров на X. Факторгруппа  наз. группой классов дивизоров и обозначается через Сl(Х). Группа Сl(Х) изоморфна группе Pic (X).классов одномерных векторных расслоений на X(см. Векторное алгебраическое расслоение). Степень главных дивизоров на г. п. к. равна нулю, поэтому все дивизоры из одного класса имеют одну и ту же степень. В частности, можно говорить о степени класса дивизоров и о подгруппе
наз. группой классов дивизоров и обозначается через Сl(Х). Группа Сl(Х) изоморфна группе Pic (X).классов одномерных векторных расслоений на X(см. Векторное алгебраическое расслоение). Степень главных дивизоров на г. п. к. равна нулю, поэтому все дивизоры из одного класса имеют одну и ту же степень. В частности, можно говорить о степени класса дивизоров и о подгруппе  классов дивизоров степени 0. Справедливо следующее равенство:
классов дивизоров степени 0. Справедливо следующее равенство:

Для прямой  т. е. любой дивизор степени 0 является главным. Это свойство характерно для рациональных г. п. к.
т. е. любой дивизор степени 0 является главным. Это свойство характерно для рациональных г. п. к.
Для любой полной А. к. Xчисло  наз. арифметическимродом А. к. X. Если X - гладкая, то я совпадает с размерностью пространства
наз. арифметическимродом А. к. X. Если X - гладкая, то я совпадает с размерностью пространства  всех регулярных дифференциальных форм на X, эта размерность наз. родом А. к. X. По определению, род А. к. равен роду ее неособой модели. Для любого неотрицательного целого числа gсуществует А. к. рода g. Рациональные кривые характеризуются равенством g=0. Если Xпроективная плоская кривая порядка т, то
всех регулярных дифференциальных форм на X, эта размерность наз. родом А. к. X. По определению, род А. к. равен роду ее неособой модели. Для любого неотрицательного целого числа gсуществует А. к. рода g. Рациональные кривые характеризуются равенством g=0. Если Xпроективная плоская кривая порядка т, то

а ее род вычисляется по формуле:

где d- неотрицательное целое число, измеряющее отклонение от гладкости на X. Если Xимеет только обыкновенные двойные точки, то dесть просто число особых точек. В частности, плоская г. п. к. имеет род

откуда следует, что не всякая г. п. к. является плоской. Для пространственной кривой Xимеет место оценка

где п - степень X. Кривые n-й степени максимального рода существуют для каждого значения пи лежат на квадрике (М. Альфаи, М. Alphen, 1870, см. [8]).
Степень канонич. класса  г. п. к. Xсвязана с родом кривой формулой deg
г. п. к. Xсвязана с родом кривой формулой deg  Если г. п. к. Xлежит на гладкой алгебраич. поверхности F, то имеет место формула присоединения:
Если г. п. к. Xлежит на гладкой алгебраич. поверхности F, то имеет место формула присоединения: 
 В частности,
В частности, Для произвольного дивизора Dна Xможно рассмотреть подмножество поля k(X), состоящее из нуля и тех функций f, для к-рых
Для произвольного дивизора Dна Xможно рассмотреть подмножество поля k(X), состоящее из нуля и тех функций f, для к-рых  Это-линейное пространство над kконечной размерности l(D). Размерность полной линейной системы, определяемой дивизором D, равна l(D) -1. Вычисление размерности l(D).является важной задачей теории А. к. Наиболее сильный результат в этом направлении - Римана - Роха теорема. Для г. п. к. эта теорема заключается в равенстве:
Это-линейное пространство над kконечной размерности l(D). Размерность полной линейной системы, определяемой дивизором D, равна l(D) -1. Вычисление размерности l(D).является важной задачей теории А. к. Наиболее сильный результат в этом направлении - Римана - Роха теорема. Для г. п. к. эта теорема заключается в равенстве:

где g - род кривой X. В случае, когда  (соответственно
(соответственно 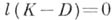 ), говорят, что дивизор D специальный (соответственно неспециальный). Для неспециальных дивизоров теорема Римана - Роха дает равенство
), говорят, что дивизор D специальный (соответственно неспециальный). Для неспециальных дивизоров теорема Римана - Роха дает равенство  Каждый дивизор степени большей 2g- 2 является неспециальным.
Каждый дивизор степени большей 2g- 2 является неспециальным.
Класс дивизоров, линейно эквивалентных дивизору Dна г. п. к. X, определяет точку на Якоби многообразии J(X).А. к. X. Это многообразие совпадает с Алъбанезе многообразием и Пикара многообразием А. к. X. Точки, соответствующие классам специальных дивизоров 1, есть особые точки Пуанкаре дивизора на J(X). Если  обозначает подмножество точек J(X), соответствующих классам дивизоров Dс deg D = n и l(D)=r, то
обозначает подмножество точек J(X), соответствующих классам дивизоров Dс deg D = n и l(D)=r, то 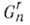 образует подсхему в J(X).и
образует подсхему в J(X).и

(теорема Римана - Брилля - Нётера). Эта теорема имеет многочисленные применения, одним из к-рых является следующее. Всякий дивизор D, для к-рого  определяет рациональное отображение
определяет рациональное отображение 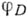 кривой Xв проективное пространство
кривой Xв проективное пространство 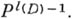 Отображение
Отображение 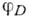 зависит от класса D. Если
зависит от класса D. Если  то
то  определяет изоморфное вложение кривой Xв Р т, причем
определяет изоморфное вложение кривой Xв Р т, причем  не содержится ни в каком собственном подпространстве пространства
не содержится ни в каком собственном подпространстве пространства 
 . Наиболее интересным с точки зрения бирациональной классификации кривых являются отображения
. Наиболее интересным с точки зрения бирациональной классификации кривых являются отображения  , соответствующие кратности пК канонич. класса кривой X. При
, соответствующие кратности пК канонич. класса кривой X. При 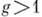 класс 3K определяет изоморфное вложение г. п. к. в
класс 3K определяет изоморфное вложение г. п. к. в  При этом кривые
При этом кривые 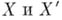 бирационально эквивалентны тогда и только тогда, когда их образы
бирационально эквивалентны тогда и только тогда, когда их образы  получаются друг из друга проективным преобразованием пространства
получаются друг из друга проективным преобразованием пространства 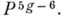 Исследование отображения
Исследование отображения  позволило получить более тонкую характеристику кривых рода
позволило получить более тонкую характеристику кривых рода  Для этих кривых отображение
Для этих кривых отображение  будет изоморфным вложением в том и только том случае, когда Xне является гиперэллиптической кривой. В случае, когда
будет изоморфным вложением в том и только том случае, когда Xне является гиперэллиптической кривой. В случае, когда 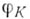 - изоморфизм, кривая
- изоморфизм, кривая  наз. канонической; она определена однозначно с точностью до проективных преобразований в
наз. канонической; она определена однозначно с точностью до проективных преобразований в 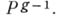 Важнейшей задачей теории А. к. является классификация кривых с точностью до бирационального изоморфизма. В этом направлении получен ряд сильных результатов, но исчерпывающего решения задачи пока (1977) не имеется. Г. п. к. можно разбить на следующие 4 класса:
Важнейшей задачей теории А. к. является классификация кривых с точностью до бирационального изоморфизма. В этом направлении получен ряд сильных результатов, но исчерпывающего решения задачи пока (1977) не имеется. Г. п. к. можно разбить на следующие 4 класса:
1) кривые рода 0 бирационально эквивалентны Р';
2) кривые рода 1 (эллиптич. кривые) бирационально эквивалентны гладкой кубической кривой в .Р 2;
3) гиперэллиптич. кривые;
4) негиперэллиптич. кривые рода  бирационально эквивалентны канонич. кривой в
бирационально эквивалентны канонич. кривой в  (А. к. основного типа).
(А. к. основного типа).
Род кривой не характеризует полностью бирацио-нальный класс А. к. Единственное исключение составляют кривые рода 0. В случае, когда kесть поле комплексных чисел  множество классов изоморфных друг другу эллиптич. кривых описывается точками фак-торпространства H/G, где Н - верхняя полуплоскость, G - модулярная группа, состоящая из дробно-линейных преобразований с целыми коэффициентами и определителем, равным +1. Пространство H/G имеет строение аналитич. многообразия, изоморфного
множество классов изоморфных друг другу эллиптич. кривых описывается точками фак-торпространства H/G, где Н - верхняя полуплоскость, G - модулярная группа, состоящая из дробно-линейных преобразований с целыми коэффициентами и определителем, равным +1. Пространство H/G имеет строение аналитич. многообразия, изоморфного  (см. Эллиптическая кривая). Классы бирационально эквивалентных кривых рода g> 1 описываются точками некоторого алгебраич. многообразия Mg размерности 3g-3, называемого многообразием модулей кривых рода g. Это многообразие неприводимо. Есть гипотеза, что М g унирационально, но она доказана только для g<11 (Ф. Севери, F. Severi).
(см. Эллиптическая кривая). Классы бирационально эквивалентных кривых рода g> 1 описываются точками некоторого алгебраич. многообразия Mg размерности 3g-3, называемого многообразием модулей кривых рода g. Это многообразие неприводимо. Есть гипотеза, что М g унирационально, но она доказана только для g<11 (Ф. Севери, F. Severi).
Имеют место следующие результаты о группе Aut (X).автоморфизмов г. п. к. X.1) Если Xесть 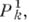 то Aut (X) - группа дробно-линейных преобразований PGL(1, k). 2).Если X - эллиптическая кривая, то Aut(AT) есть алгебраич. группа, связная компонента единицы к-рой совпадает с группой точек X(k).3) Если X - кривая рода g>l, то Aut(X) всегда конечная группа. Ее порядок ограничен числом 84(g - 1) (см. [6]). В последнем случае важную роль при изучении группы Aut(X) играют Вейерштрасса точки на X.
то Aut (X) - группа дробно-линейных преобразований PGL(1, k). 2).Если X - эллиптическая кривая, то Aut(AT) есть алгебраич. группа, связная компонента единицы к-рой совпадает с группой точек X(k).3) Если X - кривая рода g>l, то Aut(X) всегда конечная группа. Ее порядок ограничен числом 84(g - 1) (см. [6]). В последнем случае важную роль при изучении группы Aut(X) играют Вейерштрасса точки на X.
Другой способ изучения группы Aut(X) дает тот факт, что каждая г. п. к. является конечным (разветвленным) накрытием проективной прямой.
Пусть X - г. п. к., определенная над полем  Множество точек кривой
Множество точек кривой  снабжается естественным строением одномерного компактного аналитич. многообразия, к-рое наз. также компактной римановой поверхностью. Обратное тоже верно, т. е. всякая компактная риманова поверхность может быть получена из нек-рой г. п. к. Обычно употребляется один и тот же символ Xдля обозначения г. п. к. и соответствующего ей одномерного комплексного многообразия. Всякое связное комплексное многообразие представимо в виде фактора
снабжается естественным строением одномерного компактного аналитич. многообразия, к-рое наз. также компактной римановой поверхностью. Обратное тоже верно, т. е. всякая компактная риманова поверхность может быть получена из нек-рой г. п. к. Обычно употребляется один и тот же символ Xдля обозначения г. п. к. и соответствующего ей одномерного комплексного многообразия. Всякое связное комплексное многообразие представимо в виде фактора 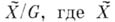 - связное односвязное комплексное многообразие, G - группа автоморфизмов многообразия
- связное односвязное комплексное многообразие, G - группа автоморфизмов многообразия  , действующая на
, действующая на  дискретно и свободно. Весьма примечательно, что одномерных связных одно-связных аналитических многообразий, с точностью до изоморфизма, всего три. Это - проективная прямая
дискретно и свободно. Весьма примечательно, что одномерных связных одно-связных аналитических многообразий, с точностью до изоморфизма, всего три. Это - проективная прямая  (риманова сфера), аффинная прямая
(риманова сфера), аффинная прямая  (конечная плоскость) и внутренность единичного круга
(конечная плоскость) и внутренность единичного круга 
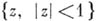 (плоскость Лобачевского). Все г. п. к. можно разбить на три класса в зависимости от того, к какому из трех типов относится их универсальная накрывающая.
(плоскость Лобачевского). Все г. п. к. можно разбить на три класса в зависимости от того, к какому из трех типов относится их универсальная накрывающая.
Вопрос о классификации г. п. к. данного типа сводится к изучению дискретных групп преобразований универсальных накрывающих, действующих свободно с относительно компактной фундаментальной областью. В случае проективной прямой G - единичная группа; в случае аффинной прямой Gизоморфна подгруппе 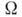 аддитивной группы
аддитивной группы 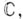 являющейся двумерной решеткой в
являющейся двумерной решеткой в  в случае внутренности единичного круга G - подгруппа движений в плоскости Лобачевского, определяемая нек-рым неевклидовым ограниченным многоугольником. Таким образом, первый класс содержит единственную кривую
в случае внутренности единичного круга G - подгруппа движений в плоскости Лобачевского, определяемая нек-рым неевклидовым ограниченным многоугольником. Таким образом, первый класс содержит единственную кривую  второй класс состоит из комплексных торов
второй класс состоит из комплексных торов  и все они имеют строение одномерного абелевого многообразия (эллиптич. кривой), причем сложение точек на торе определяет групповую структуру на соответствующей кривой. Всякая гладкая эллиптич. кривая получается таким образом. Поле рациональных функций
и все они имеют строение одномерного абелевого многообразия (эллиптич. кривой), причем сложение точек на торе определяет групповую структуру на соответствующей кривой. Всякая гладкая эллиптич. кривая получается таким образом. Поле рациональных функций 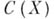 на эллиптич. кривой
на эллиптич. кривой 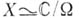 изоморфно полю мероморфных двоякопериодических (эллиптических) функций с группой периодов
изоморфно полю мероморфных двоякопериодических (эллиптических) функций с группой периодов 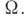 Если
Если 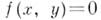 - уравнение аффинной модели кривой X, то существует его параметризация
- уравнение аффинной модели кривой X, то существует его параметризация  эллиптич. функциями (униформизация кривой X). Третий класс состоит из всех г. п. к. Xрода g>1. Поле С(X).в этом случае изоморфно полю мероморфных на Dфункций, инвариантных относительно группы G. Такие функции наз. автоморфными. Любая А. к. рода g>l униформизуется автоморфными функциями (см. Униформизация). Задача классификации эллиптич. кривых также приводила к рассмотрению фактора D/G, но там ситуация существенно отличалась от только что рассмотренной. Во-первых, группа Gимела неподвижные точки в D, во-вторых, многообразие D/G было некомпактным, хотя обладало конечной площадью по Лобачевскому. Рассмотрение в общем случае таких групп и соответствующих факторов играет важную роль в современных арифметич. исследованиях.
эллиптич. функциями (униформизация кривой X). Третий класс состоит из всех г. п. к. Xрода g>1. Поле С(X).в этом случае изоморфно полю мероморфных на Dфункций, инвариантных относительно группы G. Такие функции наз. автоморфными. Любая А. к. рода g>l униформизуется автоморфными функциями (см. Униформизация). Задача классификации эллиптич. кривых также приводила к рассмотрению фактора D/G, но там ситуация существенно отличалась от только что рассмотренной. Во-первых, группа Gимела неподвижные точки в D, во-вторых, многообразие D/G было некомпактным, хотя обладало конечной площадью по Лобачевскому. Рассмотрение в общем случае таких групп и соответствующих факторов играет важную роль в современных арифметич. исследованиях.
Если А. к. Xопределена над незамкнутым полем k, то одним из важнейших является вопрос о существовании и нахождении рациональных точек X(k).кривой X. Для г. п. к. Xнад конечным полем kдоказано неравенство  где N - число точек кривой X, рациональных над конечным расширением Lполя k, q - число элементов поля L,a g- род кривой X. Это неравенство эквивалентно гипотезе, Римана о нулях
где N - число точек кривой X, рациональных над конечным расширением Lполя k, q - число элементов поля L,a g- род кривой X. Это неравенство эквивалентно гипотезе, Римана о нулях 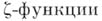 кривой X - все нули
кривой X - все нули  лежат на вертикальной прямой s = 1/2 (см. Дзета-функция в алгебраич. геометрии).
лежат на вертикальной прямой s = 1/2 (см. Дзета-функция в алгебраич. геометрии).
Пусть теперь X - А. к., определенная над полем рациональных чисел  Тогда для кривых рода 0 точки
Тогда для кривых рода 0 точки 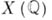 находятся сравнительно легко, для эллиптич. кривых рациональные точки составляют группу с конечным числом образующих (если
находятся сравнительно легко, для эллиптич. кривых рациональные точки составляют группу с конечным числом образующих (если  не пусто), для кривых рода
не пусто), для кривых рода  имеется пока не доказанная (1977) Морделла гипотеза о том, что
имеется пока не доказанная (1977) Морделла гипотеза о том, что  конечно.
конечно.
Если основное поле kесть поле рациональных функций k0(B).г. п. к. B, то каждая г. п. к. Xнад kизоморфна общему слою  морфизма
морфизма  гладкой проективной алгебраич. поверхности Vнад k0. Этот морфизм будет однозначно определен, если потребовать, чтобы в его слоях не было исключительных кривых рода 1. Множество рациональных точек
гладкой проективной алгебраич. поверхности Vнад k0. Этот морфизм будет однозначно определен, если потребовать, чтобы в его слоях не было исключительных кривых рода 1. Множество рациональных точек  находится в биективном соответствии с множеством сечений V(В).морфизма
находится в биективном соответствии с множеством сечений V(В).морфизма  конечно для кривых рода
конечно для кривых рода  Кривые рода 0 и 1 над полем
Кривые рода 0 и 1 над полем  изучаются в теории алгебраич. поверхностей (см. Эллиптическая поверхность, Линейчатая поверхность).
изучаются в теории алгебраич. поверхностей (см. Эллиптическая поверхность, Линейчатая поверхность).
Лит.:[1]Шафаревич И. Р., Основы алгебраической геометрии, М., 1972; [2] Уонер Р., Алгебраические кривые, пер. с англ., М., 1952; [3] Мамфорд Д., Лекции о кривых на алгебраической поверхности, пер. с англ., М., 1968; [4] Шевалле К., Введение в теорию алгебраических функций от одной переменной, пер. с англ., М., 1959; [5] Серр Ж.-П., Алгебраические группы и поля классов, пер. с франц., М., 1968; [6] Чеботарев Н. Г., Теория алгебраических функций, М.- Л., 1948; [7] Спрингер Д ж., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [8] Итоги науки и техники. Алгебра. Топология. Геометрия, т. 12, М., 1974, с. 77 -170. В. <Е. <Воскресенский.

 удовлетворяющих уравнению
удовлетворяющих уравнению 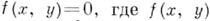 - многочлен с коэффициентами из алгебраически замкнутого поля k. Поле рациональных функций неприводимой А. к. над kесть поле алгебраич. функций одного переменного и имеет вид
- многочлен с коэффициентами из алгебраически замкнутого поля k. Поле рациональных функций неприводимой А. к. над kесть поле алгебраич. функций одного переменного и имеет вид  где хи усвязаны уравнением
где хи усвязаны уравнением 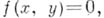 а
а 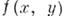 - многочлен над k. Это означает, что всякая А. к. бирационально изоморфна плоской аффинной кривой.
- многочлен над k. Это означает, что всякая А. к. бирационально изоморфна плоской аффинной кривой. с последующим замыканием в Зариского топологии. Таким образом получается проективная кривая X, причем исходная аффинная кривая У может быть получена из Xвыбрасыванием конечного числа точек. Если Yнеприводима, то Xи Y бирационально изоморфны. Каждая полная А. к. является проективной. Если X - гладкая проективная кривая (г. п. к.), то все кольца нормирования поля
с последующим замыканием в Зариского топологии. Таким образом получается проективная кривая X, причем исходная аффинная кривая У может быть получена из Xвыбрасыванием конечного числа точек. Если Yнеприводима, то Xи Y бирационально изоморфны. Каждая полная А. к. является проективной. Если X - гладкая проективная кривая (г. п. к.), то все кольца нормирования поля 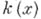 исчерпываются локальными кольцами
исчерпываются локальными кольцами Если две г. п. к. бирационально эквивалентны, то они изоморфны. Нормальная А. к. является гладкой. В частности, всякая неприводимая А. к. бирационально эквивалентна г. п. к. Получаемая в процессе нормализации гладкая проективная модель А. к. лежит в нек-ром пространстве
Если две г. п. к. бирационально эквивалентны, то они изоморфны. Нормальная А. к. является гладкой. В частности, всякая неприводимая А. к. бирационально эквивалентна г. п. к. Получаемая в процессе нормализации гладкая проективная модель А. к. лежит в нек-ром пространстве  Любая г. п. к. изоморфна кривой, расположенной в
Любая г. п. к. изоморфна кривой, расположенной в  Каждая плоская А. к. кремоновым преобразованием может быть преобразована в кривую с обыкновенными особыми точками.
Каждая плоская А. к. кремоновым преобразованием может быть преобразована в кривую с обыкновенными особыми точками.
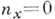 почти для всех х. Если все
почти для всех х. Если все  то дивизор Dназ. положительным, или эффективным, что обозначается
то дивизор Dназ. положительным, или эффективным, что обозначается  Степенью дивизора D наз. число
Степенью дивизора D наз. число 
 наз. группой классов дивизоров и обозначается через Сl(Х). Группа Сl(Х) изоморфна группе Pic (X).классов одномерных векторных расслоений на X(см. Векторное алгебраическое расслоение). Степень главных дивизоров на г. п. к. равна нулю, поэтому все дивизоры из одного класса имеют одну и ту же степень. В частности, можно говорить о степени класса дивизоров и о подгруппе
наз. группой классов дивизоров и обозначается через Сl(Х). Группа Сl(Х) изоморфна группе Pic (X).классов одномерных векторных расслоений на X(см. Векторное алгебраическое расслоение). Степень главных дивизоров на г. п. к. равна нулю, поэтому все дивизоры из одного класса имеют одну и ту же степень. В частности, можно говорить о степени класса дивизоров и о подгруппе  классов дивизоров степени 0. Справедливо следующее равенство:
классов дивизоров степени 0. Справедливо следующее равенство:
 т. е. любой дивизор степени 0 является главным. Это свойство характерно для рациональных г. п. к.
т. е. любой дивизор степени 0 является главным. Это свойство характерно для рациональных г. п. к. наз. арифметическимродом А. к. X. Если X - гладкая, то я совпадает с размерностью пространства
наз. арифметическимродом А. к. X. Если X - гладкая, то я совпадает с размерностью пространства  всех регулярных дифференциальных форм на X, эта размерность наз. родом А. к. X. По определению, род А. к. равен роду ее неособой модели. Для любого неотрицательного целого числа gсуществует А. к. рода g. Рациональные кривые характеризуются равенством g=0. Если Xпроективная плоская кривая порядка т, то
всех регулярных дифференциальных форм на X, эта размерность наз. родом А. к. X. По определению, род А. к. равен роду ее неособой модели. Для любого неотрицательного целого числа gсуществует А. к. рода g. Рациональные кривые характеризуются равенством g=0. Если Xпроективная плоская кривая порядка т, то 



 г. п. к. Xсвязана с родом кривой формулой deg
г. п. к. Xсвязана с родом кривой формулой deg  Если г. п. к. Xлежит на гладкой алгебраич. поверхности F, то имеет место формула присоединения:
Если г. п. к. Xлежит на гладкой алгебраич. поверхности F, то имеет место формула присоединения: 
 В частности,
В частности, Для произвольного дивизора Dна Xможно рассмотреть подмножество поля k(X), состоящее из нуля и тех функций f, для к-рых
Для произвольного дивизора Dна Xможно рассмотреть подмножество поля k(X), состоящее из нуля и тех функций f, для к-рых  Это-линейное пространство над kконечной размерности l(D). Размерность полной линейной системы, определяемой дивизором D, равна l(D) -1. Вычисление размерности l(D).является важной задачей теории А. к. Наиболее сильный результат в этом направлении - Римана - Роха теорема. Для г. п. к. эта теорема заключается в равенстве:
Это-линейное пространство над kконечной размерности l(D). Размерность полной линейной системы, определяемой дивизором D, равна l(D) -1. Вычисление размерности l(D).является важной задачей теории А. к. Наиболее сильный результат в этом направлении - Римана - Роха теорема. Для г. п. к. эта теорема заключается в равенстве:
 (соответственно
(соответственно 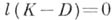 ), говорят, что дивизор D специальный (соответственно неспециальный). Для неспециальных дивизоров теорема Римана - Роха дает равенство
), говорят, что дивизор D специальный (соответственно неспециальный). Для неспециальных дивизоров теорема Римана - Роха дает равенство  Каждый дивизор степени большей 2g- 2 является неспециальным.
Каждый дивизор степени большей 2g- 2 является неспециальным. обозначает подмножество точек J(X), соответствующих классам дивизоров Dс deg D = n и l(D)=r, то
обозначает подмножество точек J(X), соответствующих классам дивизоров Dс deg D = n и l(D)=r, то 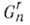 образует подсхему в J(X).и
образует подсхему в J(X).и 
 определяет рациональное отображение
определяет рациональное отображение 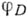 кривой Xв проективное пространство
кривой Xв проективное пространство 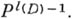 Отображение
Отображение 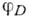 зависит от класса D. Если
зависит от класса D. Если  то
то  определяет изоморфное вложение кривой Xв Р т, причем
определяет изоморфное вложение кривой Xв Р т, причем  не содержится ни в каком собственном подпространстве пространства
не содержится ни в каком собственном подпространстве пространства 
 . Наиболее интересным с точки зрения бирациональной классификации кривых являются отображения
. Наиболее интересным с точки зрения бирациональной классификации кривых являются отображения  , соответствующие кратности пК канонич. класса кривой X. При
, соответствующие кратности пК канонич. класса кривой X. При 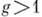 класс 3K определяет изоморфное вложение г. п. к. в
класс 3K определяет изоморфное вложение г. п. к. в  При этом кривые
При этом кривые 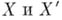 бирационально эквивалентны тогда и только тогда, когда их образы
бирационально эквивалентны тогда и только тогда, когда их образы  получаются друг из друга проективным преобразованием пространства
получаются друг из друга проективным преобразованием пространства 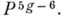 Исследование отображения
Исследование отображения  позволило получить более тонкую характеристику кривых рода
позволило получить более тонкую характеристику кривых рода  Для этих кривых отображение
Для этих кривых отображение  будет изоморфным вложением в том и только том случае, когда Xне является гиперэллиптической кривой. В случае, когда
будет изоморфным вложением в том и только том случае, когда Xне является гиперэллиптической кривой. В случае, когда 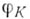 - изоморфизм, кривая
- изоморфизм, кривая  наз. канонической; она определена однозначно с точностью до проективных преобразований в
наз. канонической; она определена однозначно с точностью до проективных преобразований в 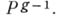 Важнейшей задачей теории А. к. является классификация кривых с точностью до бирационального изоморфизма. В этом направлении получен ряд сильных результатов, но исчерпывающего решения задачи пока (1977) не имеется. Г. п. к. можно разбить на следующие 4 класса:
Важнейшей задачей теории А. к. является классификация кривых с точностью до бирационального изоморфизма. В этом направлении получен ряд сильных результатов, но исчерпывающего решения задачи пока (1977) не имеется. Г. п. к. можно разбить на следующие 4 класса: бирационально эквивалентны канонич. кривой в
бирационально эквивалентны канонич. кривой в  (А. к. основного типа).
(А. к. основного типа). множество классов изоморфных друг другу эллиптич. кривых описывается точками фак-торпространства H/G, где Н - верхняя полуплоскость, G - модулярная группа, состоящая из дробно-линейных преобразований с целыми коэффициентами и определителем, равным +1. Пространство H/G имеет строение аналитич. многообразия, изоморфного
множество классов изоморфных друг другу эллиптич. кривых описывается точками фак-торпространства H/G, где Н - верхняя полуплоскость, G - модулярная группа, состоящая из дробно-линейных преобразований с целыми коэффициентами и определителем, равным +1. Пространство H/G имеет строение аналитич. многообразия, изоморфного  (см. Эллиптическая кривая). Классы бирационально эквивалентных кривых рода g> 1 описываются точками некоторого алгебраич. многообразия Mg размерности 3g-3, называемого многообразием модулей кривых рода g. Это многообразие неприводимо. Есть гипотеза, что М g унирационально, но она доказана только для g<11 (Ф. Севери, F. Severi).
(см. Эллиптическая кривая). Классы бирационально эквивалентных кривых рода g> 1 описываются точками некоторого алгебраич. многообразия Mg размерности 3g-3, называемого многообразием модулей кривых рода g. Это многообразие неприводимо. Есть гипотеза, что М g унирационально, но она доказана только для g<11 (Ф. Севери, F. Severi).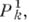 то Aut (X) - группа дробно-линейных преобразований PGL(1, k). 2).Если X - эллиптическая кривая, то Aut(AT) есть алгебраич. группа, связная
то Aut (X) - группа дробно-линейных преобразований PGL(1, k). 2).Если X - эллиптическая кривая, то Aut(AT) есть алгебраич. группа, связная  Множество точек кривой
Множество точек кривой  снабжается естественным строением одномерного компактного аналитич. многообразия, к-рое наз. также компактной римановой поверхностью. Обратное тоже верно, т. е. всякая компактная риманова поверхность может быть получена из нек-рой г. п. к. Обычно употребляется один и тот же символ Xдля обозначения г. п. к. и соответствующего ей одномерного комплексного многообразия. Всякое связное комплексное многообразие представимо в виде фактора
снабжается естественным строением одномерного компактного аналитич. многообразия, к-рое наз. также компактной римановой поверхностью. Обратное тоже верно, т. е. всякая компактная риманова поверхность может быть получена из нек-рой г. п. к. Обычно употребляется один и тот же символ Xдля обозначения г. п. к. и соответствующего ей одномерного комплексного многообразия. Всякое связное комплексное многообразие представимо в виде фактора 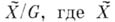 - связное односвязное комплексное многообразие, G - группа автоморфизмов многообразия
- связное односвязное комплексное многообразие, G - группа автоморфизмов многообразия  , действующая на
, действующая на  дискретно и свободно. Весьма примечательно, что одномерных связных одно-связных аналитических многообразий, с точностью до изоморфизма, всего три. Это - проективная прямая
дискретно и свободно. Весьма примечательно, что одномерных связных одно-связных аналитических многообразий, с точностью до изоморфизма, всего три. Это - проективная прямая  (риманова сфера), аффинная прямая
(риманова сфера), аффинная прямая  (конечная плоскость) и внутренность единичного круга
(конечная плоскость) и внутренность единичного круга 
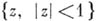 (плоскость Лобачевского). Все г. п. к. можно разбить на три класса в зависимости от того, к какому из трех типов относится их универсальная накрывающая.
(плоскость Лобачевского). Все г. п. к. можно разбить на три класса в зависимости от того, к какому из трех типов относится их универсальная накрывающая.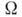 аддитивной группы
аддитивной группы 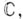 являющейся двумерной решеткой в
являющейся двумерной решеткой в  в случае внутренности единичного круга G - подгруппа движений в плоскости Лобачевского, определяемая нек-рым неевклидовым ограниченным многоугольником. Таким образом, первый класс содержит единственную кривую
в случае внутренности единичного круга G - подгруппа движений в плоскости Лобачевского, определяемая нек-рым неевклидовым ограниченным многоугольником. Таким образом, первый класс содержит единственную кривую  второй класс состоит из комплексных торов
второй класс состоит из комплексных торов  и все они имеют строение одномерного абелевого многообразия (эллиптич. кривой), причем сложение точек на торе определяет групповую структуру на соответствующей кривой. Всякая гладкая эллиптич. кривая получается таким образом. Поле рациональных функций
и все они имеют строение одномерного абелевого многообразия (эллиптич. кривой), причем сложение точек на торе определяет групповую структуру на соответствующей кривой. Всякая гладкая эллиптич. кривая получается таким образом. Поле рациональных функций 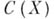 на эллиптич. кривой
на эллиптич. кривой 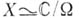 изоморфно полю мероморфных двоякопериодических (эллиптических) функций с группой периодов
изоморфно полю мероморфных двоякопериодических (эллиптических) функций с группой периодов 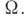 Если
Если 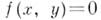 - уравнение аффинной модели кривой X, то существует его параметризация
- уравнение аффинной модели кривой X, то существует его параметризация  эллиптич. функциями (униформизация кривой X). Третий класс состоит из всех г. п. к. Xрода g>1. Поле С(X).в этом случае изоморфно полю мероморфных на Dфункций, инвариантных относительно группы G. Такие функции наз. автоморфными. Любая А. к. рода g>l униформизуется автоморфными функциями (см. Униформизация). Задача классификации эллиптич. кривых также приводила к рассмотрению фактора D/G, но там ситуация существенно отличалась от только что рассмотренной. Во-первых, группа Gимела неподвижные точки в D, во-вторых, многообразие D/G было некомпактным, хотя обладало конечной площадью по Лобачевскому. Рассмотрение в общем случае таких групп и соответствующих факторов играет важную роль в современных арифметич. исследованиях.
эллиптич. функциями (униформизация кривой X). Третий класс состоит из всех г. п. к. Xрода g>1. Поле С(X).в этом случае изоморфно полю мероморфных на Dфункций, инвариантных относительно группы G. Такие функции наз. автоморфными. Любая А. к. рода g>l униформизуется автоморфными функциями (см. Униформизация). Задача классификации эллиптич. кривых также приводила к рассмотрению фактора D/G, но там ситуация существенно отличалась от только что рассмотренной. Во-первых, группа Gимела неподвижные точки в D, во-вторых, многообразие D/G было некомпактным, хотя обладало конечной площадью по Лобачевскому. Рассмотрение в общем случае таких групп и соответствующих факторов играет важную роль в современных арифметич. исследованиях. где N - число точек кривой X, рациональных над конечным расширением Lполя k, q - число элементов поля L,a g- род кривой X. Это неравенство эквивалентно гипотезе, Римана о нулях
где N - число точек кривой X, рациональных над конечным расширением Lполя k, q - число элементов поля L,a g- род кривой X. Это неравенство эквивалентно гипотезе, Римана о нулях 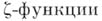 кривой X - все нули
кривой X - все нули  лежат на вертикальной прямой s = 1/2 (см. Дзета-функция в алгебраич. геометрии).
лежат на вертикальной прямой s = 1/2 (см. Дзета-функция в алгебраич. геометрии). Тогда для кривых рода 0 точки
Тогда для кривых рода 0 точки 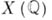 находятся сравнительно легко, для эллиптич. кривых рациональные точки составляют группу с конечным числом образующих (если
находятся сравнительно легко, для эллиптич. кривых рациональные точки составляют группу с конечным числом образующих (если  не пусто), для кривых рода
не пусто), для кривых рода  имеется пока не доказанная (1977) Морделла гипотеза о том, что
имеется пока не доказанная (1977) Морделла гипотеза о том, что  конечно.
конечно. морфизма
морфизма  гладкой проективной алгебраич. поверхности Vнад k0. Этот морфизм будет однозначно определен, если потребовать, чтобы в его слоях не было исключительных кривых рода 1. Множество рациональных точек
гладкой проективной алгебраич. поверхности Vнад k0. Этот морфизм будет однозначно определен, если потребовать, чтобы в его слоях не было исключительных кривых рода 1. Множество рациональных точек  находится в биективном соответствии с множеством сечений V(В).морфизма
находится в биективном соответствии с множеством сечений V(В).морфизма  конечно для кривых рода
конечно для кривых рода  Кривые рода 0 и 1 над полем
Кривые рода 0 и 1 над полем  изучаются в теории алгебраич. поверхностей (см. Эллиптическая поверхность, Линейчатая поверхность).
изучаются в теории алгебраич. поверхностей (см. Эллиптическая поверхность, Линейчатая поверхность).