"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУКСОВА ГРУППА
Значение ФУКСОВА ГРУППА в математической энциклопедии:
- дискретная группа голоморфных преобразований (открытого) круга Кна сфере Римана, т. е. круга или полуплоскости на комплексной плоскости. Чаще всего в качестве Кберут верхнюю полуплоскость  или единичный круг
или единичный круг

В первом случае элементы Ф. г. являются дробно-линейными преобразованиями  с действительными коэффициентами, и Ф. г. представляет собой не что иное, как дискретную подгруппу группы PSL2. Во втором случае элементы Ф. г. являются дробно-линейными преобразованиями с псевдоунитарными матрицами.
с действительными коэффициентами, и Ф. г. представляет собой не что иное, как дискретную подгруппу группы PSL2. Во втором случае элементы Ф. г. являются дробно-линейными преобразованиями с псевдоунитарными матрицами.
Если рассматривать круг Ккак конформную модель плоскости Лобачевского, то Ф. г. может быть определена как дискретная группа его движений, сохраняющих ориентацию. Ф. г. представляют собой частный случай клейновых групп.
Произвольные Ф. г. впервые рассматривались А. Пуанкаре (Н. Poincare, см. [2]) в 1882 в связи с проблемой униформизации. Группы были названы им фуксовыми в честь Л. Фукса, работа [1] к-рого стимулировала введение этого понятия. Для описания Ф. г. Пуанкаре применил комбинаторно-геометрич. метод, ставший впоследствии одним из основных методов теории дискретных групп преобразований. Понятие Ф. г. послужило основой для теории автоморфных функций, созданной А. Пуанкаре и Ф. Клейном (F. Klein).
Ф. г., сохраняющая какую-либо точку в замыкании  круга Кили прямую в смысле геометрии Лобачевского, наз. элементарной. Если Г - неэлементарная Ф. г., то множество L(Г)предельных точек орбиты точки
круга Кили прямую в смысле геометрии Лобачевского, наз. элементарной. Если Г - неэлементарная Ф. г., то множество L(Г)предельных точек орбиты точки  лежащее на граничной окружности
лежащее на граничной окружности  не зависит от хи наз. предельным множеством группы Г. Группа Г наз. Ф. г. 1-го рода, если
не зависит от хи наз. предельным множеством группы Г. Группа Г наз. Ф. г. 1-го рода, если  и 2-го рода - в противном случае (тогда L(Г) - нигде не плотное совершенное подмножество в
и 2-го рода - в противном случае (тогда L(Г) - нигде не плотное совершенное подмножество в 
Конечно порожденная Ф. г. является Ф. г. 1-го рода тогда и только тогда, когда площадь (в смысле геометрии Лобачевского) ее фундаментальной области конечна. В качестве фундаментальной области такой группы Г всегда может быть выбран выпуклый многоугольник Рплоскости Лобачевского со сторонами a1, b'1, a'1, b1 ..., ag, b'g, a'g, bg, с1, с'1, ..., с n, с'п таким образом, что

для нек-рых элементов

порождающих группу Г с определяющими соотношениями

где ki- целое число  или
или  Элемент
Элемент  оставляет на месте вершину С i многоугольника Р, общую сторонам с i и c'i. Он является эллиптическим, если
оставляет на месте вершину С i многоугольника Р, общую сторонам с i и c'i. Он является эллиптическим, если  и параболическим, если
и параболическим, если  в последнем случае вершина С i лежит на окружности
в последнем случае вершина С i лежит на окружности  т. е. является бесконечно удаленной точкой плоскости Лобачевского. Всякий эллиптич. или параболич. элемент группы Г сопряжен степени нек-рого однозначно определенного образующего
т. е. является бесконечно удаленной точкой плоскости Лобачевского. Всякий эллиптич. или параболич. элемент группы Г сопряжен степени нек-рого однозначно определенного образующего  Углы многоугольника Рпри вершинах С i, i=1, ..., п, равны
Углы многоугольника Рпри вершинах С i, i=1, ..., п, равны 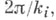 сумма всех остальных углов равна
сумма всех остальных углов равна  Стороны а i и а'i, а также bi и b'i, ci и c'i имеют одинаковую длину. Обратно, всякий выпуклый многоугольник на плоскости Лобачевского, удовлетворяющий этим условиям, является фундаментальным многоугольником описанного выше типа нек-рой конечно порожденной Ф. г. 1-го рода.
Стороны а i и а'i, а также bi и b'i, ci и c'i имеют одинаковую длину. Обратно, всякий выпуклый многоугольник на плоскости Лобачевского, удовлетворяющий этим условиям, является фундаментальным многоугольником описанного выше типа нек-рой конечно порожденной Ф. г. 1-го рода.
Всякая система образующих группы Г, к-рая получается описанным способом, наз. стандартной. При абстрактном изоморфизме конечно порожденных Ф. г. 1-го рода, отображающем множество параболич. элементов одной группы на множество параболич. элементов другой группы, всякая стандартная система образующих переходит в стандартную систему образующих.
Площадь фундаментальной области группы Г равна -  где
где

Набор чисел (g; k1,..., kn), где k1,..., kn считаются неупорядоченными, является топологич. инвариантом группы Г как группы гомеоморфизмов круга и наз. ее сигнатурой. Единственным ограничением на сигнатуру является условие

Для подгруппы  конечного индекса Ф. г. Г имеет место формула Римана - Гурвица:
конечного индекса Ф. г. Г имеет место формула Римана - Гурвица:

Во всякой Ф. г. существует подгруппа конечного индекса, не имеющая элементов конечного порядка.
Факторпространство К/Г компактифицируется путем добавления конечного числа точек, соответствующих бесконечно удаленным вершинам фундаментального многоугольника. На компактифицированном пространстве . имеется единственная комплексная структура, для к-рой отображение факторизации  голоморфно. При этом Sявляется римановой поверхностью рода g, а отображение р- регулярным разветвленным накрытием с индексами ветвления k1, ..., kn. Обратно, теорема униформизации утверждает, что для любой компактной римановой поверхности Sрода gс отмеченными точками х 1, ..., х п и для любых k1 ... ...,kn(ki- целое число
голоморфно. При этом Sявляется римановой поверхностью рода g, а отображение р- регулярным разветвленным накрытием с индексами ветвления k1, ..., kn. Обратно, теорема униформизации утверждает, что для любой компактной римановой поверхности Sрода gс отмеченными точками х 1, ..., х п и для любых k1 ... ...,kn(ki- целое число  или
или  удовлетворяющих условию (*), существует регулярное голоморфное разветвленное накрытие
удовлетворяющих условию (*), существует регулярное голоморфное разветвленное накрытие  ветвящееся в точности над точками x1, ..., х п с индексами ветвления k1, ... ..., kn соответственно. Накрытие ропределено однозначно с точностью до автоморфизма круга К. Его группа скольжений есть Ф. г. сигнатуры (g; k1, ..., kn).
ветвящееся в точности над точками x1, ..., х п с индексами ветвления k1, ... ..., kn соответственно. Накрытие ропределено однозначно с точностью до автоморфизма круга К. Его группа скольжений есть Ф. г. сигнатуры (g; k1, ..., kn).
Конечно порожденные Ф. г. 1-го рода фиксированной сигнатуры (g; k1, ..., kn )могут быть параметризованы точками нек-рого (Зn-3+п)-мерного комплексного многообразия, гомеоморфного клетке,- т. н. пространства Тайхмюллера .(g; k1,...,kn) (см. [4]). При атом двум точкам пространства Тайхмюллера соответствует одна и та же (с точностью до сопряженности в группе автоморфизмов круга) Ф. г. тогда и только тогда, когда эти точки эквивалентны относительно нек-рой дискретной группы голоморфных преобразований пространства Т(g; k1, ..., kn )-т. н. модулярной группы Mod (g; k1...., kn). Имеется изоморфизм

при к-ром группа Mod (g; kl, ..., kn )переходит в подгруппу конечного индекса группы 
Если Ф. г. сигнатуры (g; k1, ..., kn )содержит подгруппу конечного индекса сигнатуры (h; l1,..., l т), то пространство .(g; k1, .. ., kn )естественным образом вкладывается в виде замкнутого подмножества в пространство Т(h; l1, ..., lm). В нек-рых исключительных случаях эти пространства совпадают [10]. Напр., Т(2)=Т(0; 2, 2, 2, 2, 2, 2); это означает, что всякая компактная риманова поверхность рода 2 допускает гиперэллиптич. инволюцию и, значит, является гиперэллиптич. кривой.
Для Ф. г. сигнатуры (0; k1, k2, k3),называемых треугольными группами, и только для них, пространство Тайхмюллера состоит из одной точки. Всякая треугольная группа является подгруппой индекса 2 в группе, порожденной отражениями относительно сторон треугольника с углами (см. Отражений группа). Примером треугольной  группы служит модулярная группа Клейна; ее сигнатура равна
группы служит модулярная группа Клейна; ее сигнатура равна 
Всякая конечно порожденная Ф. г. 2-го рода топологически (как группа гомеоморфизмов круга) изоморфна конечно порожденной Ф. г. 1-го рода и допускает аналогичное геометрич. описание, с той разницей, что нек-рые пары сторон  фундаментального многоугольника не имеют общих точек, даже бесконечно удаленных, а соответствующие образующие
фундаментального многоугольника не имеют общих точек, даже бесконечно удаленных, а соответствующие образующие  являются гиперболич. преобразованиями. Компактифицированное факторпространство представляет собой рима-нову поверхность с краем.
являются гиперболич. преобразованиями. Компактифицированное факторпространство представляет собой рима-нову поверхность с краем.
Всякая бесконечно порожденная Ф. г. является свободным произведением циклич. подгрупп. Ее фундаментальная область может быть построена как предел фундаментальных областей конечно порожденных групп (см. [5]).
Лит.:[1] Fuchs L., лJ. reine und angew. Math.

 или единичный круг
или единичный круг 
 с действительными коэффициентами, и Ф. г. представляет собой не что иное, как дискретную подгруппу группы PSL2. Во втором случае элементы Ф. г. являются дробно-линейными преобразованиями с псевдоунитарными матрицами.
с действительными коэффициентами, и Ф. г. представляет собой не что иное, как дискретную подгруппу группы PSL2. Во втором случае элементы Ф. г. являются дробно-линейными преобразованиями с псевдоунитарными матрицами.  круга Кили прямую в смысле геометрии Лобачевского, наз. элементарной. Если Г - неэлементарная Ф. г., то множество L(Г)предельных точек орбиты точки
круга Кили прямую в смысле геометрии Лобачевского, наз. элементарной. Если Г - неэлементарная Ф. г., то множество L(Г)предельных точек орбиты точки  лежащее на граничной окружности
лежащее на граничной окружности  не зависит от хи наз. предельным множеством группы Г. Группа Г наз. Ф. г. 1-го рода, если
не зависит от хи наз. предельным множеством группы Г. Группа Г наз. Ф. г. 1-го рода, если  и 2-го рода - в противном случае (тогда L(Г) - нигде не плотное совершенное подмножество в
и 2-го рода - в противном случае (тогда L(Г) - нигде не плотное совершенное подмножество в 



 или
или  Элемент
Элемент  оставляет на месте вершину С i многоугольника Р, общую сторонам с i и c'i. Он является эллиптическим, если
оставляет на месте вершину С i многоугольника Р, общую сторонам с i и c'i. Он является эллиптическим, если  и параболическим, если
и параболическим, если  в последнем случае вершина С i лежит на окружности
в последнем случае вершина С i лежит на окружности  т. е. является бесконечно удаленной точкой плоскости Лобачевского. Всякий эллиптич. или параболич. элемент группы Г сопряжен степени нек-рого однозначно определенного образующего
т. е. является бесконечно удаленной точкой плоскости Лобачевского. Всякий эллиптич. или параболич. элемент группы Г сопряжен степени нек-рого однозначно определенного образующего  Углы многоугольника Рпри вершинах С i, i=1, ..., п, равны
Углы многоугольника Рпри вершинах С i, i=1, ..., п, равны 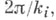 сумма всех остальных углов равна
сумма всех остальных углов равна  Стороны а i и а'i, а также bi и b'i, ci и c'i имеют одинаковую длину. Обратно, всякий выпуклый многоугольник на плоскости Лобачевского, удовлетворяющий этим условиям, является фундаментальным многоугольником описанного выше типа нек-рой конечно порожденной Ф. г. 1-го рода.
Стороны а i и а'i, а также bi и b'i, ci и c'i имеют одинаковую длину. Обратно, всякий выпуклый многоугольник на плоскости Лобачевского, удовлетворяющий этим условиям, является фундаментальным многоугольником описанного выше типа нек-рой конечно порожденной Ф. г. 1-го рода.  где
где 

 конечного индекса Ф. г. Г имеет место формула Римана - Гурвица:
конечного индекса Ф. г. Г имеет место формула Римана - Гурвица: 
 голоморфно. При этом Sявляется римановой поверхностью рода g, а отображение р- регулярным разветвленным накрытием с индексами ветвления k1, ..., kn. Обратно, теорема униформизации утверждает, что для любой компактной римановой поверхности Sрода gс отмеченными точками х 1, ..., х п и для любых k1 ... ...,kn(ki- целое число
голоморфно. При этом Sявляется римановой поверхностью рода g, а отображение р- регулярным разветвленным накрытием с индексами ветвления k1, ..., kn. Обратно, теорема униформизации утверждает, что для любой компактной римановой поверхности Sрода gс отмеченными точками х 1, ..., х п и для любых k1 ... ...,kn(ki- целое число  или
или  удовлетворяющих условию (*), существует регулярное голоморфное разветвленное накрытие
удовлетворяющих условию (*), существует регулярное голоморфное разветвленное накрытие  ветвящееся в точности над точками x1, ..., х п с индексами ветвления k1, ... ..., kn соответственно. Накрытие ропределено однозначно с точностью до автоморфизма круга К. Его группа скольжений есть Ф. г. сигнатуры (g; k1, ..., kn).
ветвящееся в точности над точками x1, ..., х п с индексами ветвления k1, ... ..., kn соответственно. Накрытие ропределено однозначно с точностью до автоморфизма круга К. Его группа скольжений есть Ф. г. сигнатуры (g; k1, ..., kn). 

 группы служит модулярная группа Клейна; ее сигнатура равна
группы служит модулярная группа Клейна; ее сигнатура равна 
 фундаментального многоугольника не имеют общих точек, даже бесконечно удаленных, а соответствующие образующие
фундаментального многоугольника не имеют общих точек, даже бесконечно удаленных, а соответствующие образующие  являются гиперболич. преобразованиями. Компактифицированное факторпространство представляет собой рима-нову поверхность с краем.
являются гиперболич. преобразованиями. Компактифицированное факторпространство представляет собой рима-нову поверхность с краем.