|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОЧТИКОЛЬЦОЗначение ПОЧТИКОЛЬЦО в математической энциклопедии: - одно из обобщений понятия ассоциативного кольца. П.- это кольцоид над группой, т. е. универсальная алгебра, в к-рой имеется ассоциативная операция умножения и операция сложения; относительно сложения П. должно быть группой (не обязательно коммутативной), причем должен также выполняться правый закон дистрибутивности: П. являются также частным случаем мультиоператорных групп. Примерами П. являются множества MS (Г).всех отображений группы Г в себя, перестановочных с действием фиксированной полугруппы эндоморфизмов Sгруппы Г. Групповые операции в М S (Г) вводятся поточечно, умножением в М S (Т).является композиция отображений. Почтикольцо MS(T) является аналогом кольца матриц. Обычным образом вводятся понятия подпочтикольца, идеала, правого модуля над П. Пусть N0 (соответственно Nc) - многообразие П., задаваемое тождеством Оx=0 (соответственно Ох=х). Любое почтикольцо Аразлагается в сумму подпочтиколец А=А 0+А с, где Оказывается, что эти радикалы обладают многими свойствами радикала Джекобсона ассоциативных колец (см. [4]). Для П. справедлив аналог теоремы Оре о почтикольцах частных [4]. Дистрибутивно порожденным почтикольцом наз. П., аддитивная группа к-рого порождается такими элементами х, что (y + z)x=yx + zx для всех у,z из П. Все дистрибутивно порожденные П. порождают многообразие N0. Для конечных дистрибутивно порожденных П. понятия 1- и 2-примитивности совпадают; 1-примитивные дистрибутивно порожденные П. имеют вид M0 (Г) для нек-рой группы Г. В дистрибутивно порожденном П., с тождеством ( ху - ух)n(x,y)= ху - ух, п( х, у)> 1, умножение коммутативно (см. [3], [4]). Каждое П. из N0, не содержащее нильпотентных элементов, является подпрямым произведением П. без делителей нуля [4]. Почтиалгебра Аразлагается в прямую сумму простых П. тогда и только тогда, когда а) она удовлетворяет условию минимальности для главных идеалов, б) в A нет идеалов с нулевым умножением, в) аннулягор любого минимального идеала максимален [1]. Для П. получены результаты, аналогичные результатам о строении регулярных колец [2], о почтикольцах частных [5]. П. имеют приложения к изучению групп подстановок, блок-схем, проективной геометрии [4]. Лит.:[1] Bell H. Е., "Canad. Math. Bull.", 1977, v. 20, .Nil, p. 25-28; [2] Heatherly H. E., "J. Indian Math. Soc.", 1974, v. 38, p. 345-54; [3] Ligh S., ",T. London Math. Soc.", 1975, v. 12, pt. 1, p. 27-31; [4] Pilz G., Near-rings, Amst., 1977; [5] Oswald A., "Proc. Edinburgh Math. Soc.", 1979, v. 22, № 2, p. 77-86; [6] Полин С. В., в кн.: Кольца, Новосиб., 1973, с. 41 - 45. В. А. Артамонов. |
|
|
|

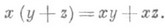
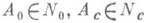 , причем
, причем  =0. Циклический правый А-модуль Мназ. примитивным типа 0, если Мпрост, примитивным типа 1, если либо хА=0, либо хА=М для любого
=0. Циклический правый А-модуль Мназ. примитивным типа 0, если Мпрост, примитивным типа 1, если либо хА=0, либо хА=М для любого  , и примитивным типа 2, если Мявляется простым A0 -модулем. Почтикольцо Аназ. примитивным типа v (v=0, 1, 2), если существует точный простой А- модуль Г типа v. При этом возникает плотное вложение почтлкольца А в М S (Г).для нек-рой полугруппы эндоморфизмов Sгруппы Г. Для 2-примитивных почтиколец Ас единицей и условием минимальности для правых идеалов в А 0 имеет место равенство А=М S (Г). (аналог теоремы Веддерберна - Артина). Для каждого v=0, 1, 2 вводится понятие радикала Джекобсона типа v, обозначаемого Jv(A), он определяется как пересечение аннуляторов v-примитивных A-модулей. Радикал J1/2 (А).определяется как пересечение максимальных правых модулярных идеалов. Все четыре радикала различны, причем
, и примитивным типа 2, если Мявляется простым A0 -модулем. Почтикольцо Аназ. примитивным типа v (v=0, 1, 2), если существует точный простой А- модуль Г типа v. При этом возникает плотное вложение почтлкольца А в М S (Г).для нек-рой полугруппы эндоморфизмов Sгруппы Г. Для 2-примитивных почтиколец Ас единицей и условием минимальности для правых идеалов в А 0 имеет место равенство А=М S (Г). (аналог теоремы Веддерберна - Артина). Для каждого v=0, 1, 2 вводится понятие радикала Джекобсона типа v, обозначаемого Jv(A), он определяется как пересечение аннуляторов v-примитивных A-модулей. Радикал J1/2 (А).определяется как пересечение максимальных правых модулярных идеалов. Все четыре радикала различны, причем 