|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОТЕНЦИАЛА ТЕОРИИ ОБРАТНЫЕ ЗАДАЧИЗначение ПОТЕНЦИАЛА ТЕОРИИ ОБРАТНЫЕ ЗАДАЧИ в математической энциклопедии: -задачи, в к-рых требуется найти форму и плотности притягивающего тела по заданным значениям внешнего (внутреннего) потенциала этого тела (см. Потенциала теория). В другой постановке одна из таких задач состоит в отыскании такого тела, чтобы его внешний объемный потенциал заданной плотности совпадал вне этого тела с заданной гармонич. функцией. Первоначально П. т. о. з. рассматривались в связи с задачами теории фигуры Земли и небесной механики. П. т. о. з. связаны с задачами фигур равновесия вращающейся жидкости и задачами геофизики. Центральное место в исследовании П. т. о. з. составляют проблемы существования, единственности, устойчивости, а также создание эффективных численных методов их решения. Теоремы существования решений в малом имеются для случая тела, близкого к данному, но при этом имеются значительные трудности в исследовании уравнений, как правило, нелинейных, к к-рым сводятся эти задачи. Критериев существования глобальных решений нет (1983). Во многих случаях существование глобальных решений предполагается заранее, что естественно во многих приложениях, и исследуются проблемы единственности и устойчивости. Одним из основных моментов в исследовании проблемы единственности является выявление дополнительных условий на решения, обеспечивающих их единственность. С проблемой единственности связана проблема устойчивости. Для задач, записанных в виде уравнения 1-го рода, вообще говоря, сколь угодно малым вариациям правой части могут соответствовать конечные вариации решений, т. е. эти задачи относятся к некорректно поставленным задачам. Для того чтобы задача стала корректной, накладывается ряд дополнительных ограничений на решения; при этих ограничениях получаются различные характеристики отклонения решения в зависимости от отклонения правой части. Ниже сформулированы обратные задачи ньютонова (объемного) потенциала и потенциала простого слоя для уравнения Лапласа в трехмерном евклидовом пространстве Пусть Т a,a- 1,2,- односвязные ограниченные области с кусочно гладкими границами Sa; где b, g - действительные числа, Общая внешняя П. т. о. з. состоит в нахождении формы и плотности притягивающего тела по заданным значениям внешнего потенциала Z(x). Для получения условий единственности решения этой задачи она формулируется следующим образом: найти такие условия для областей Т a и плотностей ma, za, чтобы из равенства внешних потенциалов Z1(x) и Z2(x). следовало равенство Решение общей внешней П. т. о. з. единственно, если П. т. о. з. для ньютоновых потенциалов получается, когда в (1) b=1 и g=0. Пусть Т a, a=1, 2,- области, звездные относительно общей точки, а функции ma (у).имеют вид ma (у).dav(у), где da=const, v>0 и не зависит от r= | у|. Если ньютоновы потенциалы удовлетворяют условию (1) и, кроме того, существует точ-ка Если в условиях (1) положить Если в условиях (1) положить Если в условиях (1) положить Общая внутренняя П. т. о. з. состоит в нахождении формы и плотностей притягивающего тела по заданным значениям внутреннего потенциала Z(x). Для получения теорем единственности используется следующая формулировка этой задачи: найти условия для областей Т a и плотностей ma, za, чтобы из совпадения внутренних потенциалов Z1(x).и Z2(x). Z1(x) = Z2(x).для следовали равенства Если в условиях (2). Пусть ищется тело Ттакое, что его внешний ньютонов потенциал U(х; Т 1,m). данной плотности m(х). равен вне тела T1 заданной гармонич. функции Н(х). Н(х). Внутренняя задача ставится аналогично внешней, причем Н(х).является решением неоднородного уравнения Лапласа в конечной области Ищется тело T1 такое, что для В отличие от внешней внутренняя задача имеет, вообще говоря, не единственное решение; число решений определяется уравнением разветвлений. Плоские П. т. о. з. ( п=2).ставятся аналогично пространственным с учетом соответствующего поведения потенциалов на бесконечности. В связи с этим ряд утверждений, приведенных выше для n=3, видоизменяется. Плоские П. т. о. з. иногда удобно исследовать методами теории функций комплексного переменного и конформных отображений. Плоская внешняя П. т. о. з. Пусть m=1 - заданная плотность, причем вместо логарифмич. потенциала масс введена его производная Решением этой задачи считается функция z(t), отображающая конформно единичный круг |t| < 1 комплексной плоскости tна область Dплоскости z=x+iy и удовлетворяющая условиям z(0)=0, z'(0)>0. Пусть D - заданная конечная односвязная область с жордановой границей, функция Ua(z)=U(z, D) для Если z(t) является решением уравнения (3), в к-ром Ua(z) заменена указанной выше функцией H(z), причем z(t) однолистна при |t|<1, z(0)=0, z'(0)>0, то H(z)=U(z, D).для |z| > R. Из уравнения (3) можно получить ряд связей между функцией Ua(z).и функцией z(t). Напр., если внешний потенциал Ua(z) можно аналитически продолжить внутрь Dчерез всю границу дD, то z(t) - аналитич. ция при |t| = l; если Это позволяет иногда решить плоскую П. т. о. з. в конечном виде. Пусть Аналогичное исследование можно провести для внешней обратной задачи логарифмич. потенциала простого слоя, а также для внутренних обратных задач логарифмич. потенциалов, причем как для внешних, так и для внутренних П. т. о. з. можно рассматривать переменные плотности. Лит.:[1] Новиков П., "Докл. АН СССР", 1938, т. 18, № 3, с. 165-68; [2] Тихонов А. Н., там же, 1943, т. 39, № 5, с. 195-98; [3] Сретенский Л. Н., Теория ньютоновского потенциала, М.-Л., 1946; [4] Иванов В. К., "Изв. АН СССР. Сер. матем.", 1956, т. 20, №6, с. 793-818; [5] его же, "Докл. АН СССР", 1955, т. 105, № 3, с. 409-11; 1956, т. 106, №4, с. 598-99; [6] Лаврентьев М. М., О некоторых некорректных задачах математической физики, Новосиб., 1962; [7] Прилепко А. И., "Дифференциальные уравнения", 1966, т. 2, № 1, с. 107-24; 1967, т. 3, № 1, с. 30- 44; 1970, т. 6, № 1, с. 27-49; 1972, т. 8, № 1, с. 118-25; его же, "Сиб. матем. ж.", 1965, т. 6, № 6, с. 1332-56; 1971, т. 12, М 3, с. 630-47; № 4, с. 828-36; Л" 6, с. 1341-53; [8] Тихонов А. Н., Арсенин В. Я., Методы решения некорректных задач, 2 изд., М., 1979. А. И. Прилепко. |
|
|
|

 , хотя указанные задачи исследуются и в n-мерном (n>2) евклидовом пространстве для потенциалов общих эллиптич. уравнений (см. [7]).
, хотя указанные задачи исследуются и в n-мерном (n>2) евклидовом пространстве для потенциалов общих эллиптич. уравнений (см. [7]). - ньютонов потенциал;
- ньютонов потенциал; - потенциал простого слоя, где | х-у| - расстояние между точками х=(x1, х 2, х 3). и у=( у 1, у 2, у 3).в
- потенциал простого слоя, где | х-у| - расстояние между точками х=(x1, х 2, х 3). и у=( у 1, у 2, у 3).в  ,
,  почти всюду в Ta(Sa). И пусть
почти всюду в Ta(Sa). И пусть 
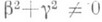
 (1)
(1) . Если множество
. Если множество  состоит из одной компоненты, то условие (1) выполняется, когда Z1(x)=Z2(x).для |x|>R, где R - достаточно большое, или когда на границе шара |x|=R задаются данные, обеспечивающие совпадение Z1(x).и Z2(x).вне этого шара. В качестве таких данных могут быть выбраны данные Дирихле на всей границе шара либо данные Коши на куске границы шара и т. д. В дальнейшем для простоты считается, что множества
состоит из одной компоненты, то условие (1) выполняется, когда Z1(x)=Z2(x).для |x|>R, где R - достаточно большое, или когда на границе шара |x|=R задаются данные, обеспечивающие совпадение Z1(x).и Z2(x).вне этого шара. В качестве таких данных могут быть выбраны данные Дирихле на всей границе шара либо данные Коши на куске границы шара и т. д. В дальнейшем для простоты считается, что множества  состоят из одной компоненты.
состоят из одной компоненты. , а области Т a контактны, т. е. такие, что для каждого из множеств Т' и Т " существует общий участок S*(mes S*
, а области Т a контактны, т. е. такие, что для каждого из множеств Т' и Т " существует общий участок S*(mes S* 0) границ Sa, причем
0) границ Sa, причем  .
. такая, что U1( х 0)= U2(x0), то Т 1=Т 2, m1=m2.
такая, что U1( х 0)= U2(x0), то Т 1=Т 2, m1=m2. , то получается задача об определении формы притягивающего тела по известным значениям внешнего ньютонова потенциала U(х).заданной плотности. Решение этой задачи единственно в классе областей Т a, звездных относительно общей точки, в случае заданных плотностей m(y), монотонно неубывающих с ростом |у|.
, то получается задача об определении формы притягивающего тела по известным значениям внешнего ньютонова потенциала U(х).заданной плотности. Решение этой задачи единственно в классе областей Т a, звездных относительно общей точки, в случае заданных плотностей m(y), монотонно неубывающих с ростом |у|. , то получается задача об определении формы притягивающего тела по известным значениям внешнего потенциала простого слоя V(х).заданной плотности z. Для выпуклых тел постоянной плотности решение этой задачи единственно.
, то получается задача об определении формы притягивающего тела по известным значениям внешнего потенциала простого слоя V(х).заданной плотности z. Для выпуклых тел постоянной плотности решение этой задачи единственно. , то получается задача об определении плотности притягивающего тела по известным значениям внешнего ньютонов потенциала. Решение задачи единственно, если
, то получается задача об определении плотности притягивающего тела по известным значениям внешнего ньютонов потенциала. Решение задачи единственно, если  функции ma(y) имеют вид
функции ma(y) имеют вид  , где
, где  (2)
(2)
 , то в классе выпуклых тел переменной положительной плотности решение единственно. Если же в условиях (2).
, то в классе выпуклых тел переменной положительной плотности решение единственно. Если же в условиях (2). const, то в классе выпуклых тел решение также единственно.
const, то в классе выпуклых тел решение также единственно. .0 при | х|
.0 при | х| . и H(х).близка в смысле нек-рой функциональной метрики к внешнему ньютонову потенциалу U(х; Т,m). заданного тела Тплотности m. Для односвязных областей Тс гладкой границей Sпри условии
. и H(х).близка в смысле нек-рой функциональной метрики к внешнему ньютонову потенциалу U(х; Т,m). заданного тела Тплотности m. Для односвязных областей Тс гладкой границей Sпри условии  решение задачи существует и единственно.
решение задачи существует и единственно.



 ; на комплексной плоскости z=x+iy вне круга К (0, R) ={|z| < R}задана аналитич. ция H(z), H(
; на комплексной плоскости z=x+iy вне круга К (0, R) ={|z| < R}задана аналитич. ция H(z), H( ) = 0, особые точки к-рой при ее аналитич. родолжении находятся внутри области
) = 0, особые точки к-рой при ее аналитич. родолжении находятся внутри области  . Требуется найти конечную односвязную область Dс жордановой границей,
. Требуется найти конечную односвязную область Dс жордановой границей,  , такую, чтобы H(z)=U(z, D).для |z|> R, где
, такую, чтобы H(z)=U(z, D).для |z|> R, где 
 . Тогда функция удовлетворяет уравнению
. Тогда функция удовлетворяет уравнению 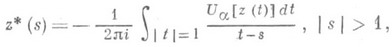 (3) где
(3) где 
 Х :^'*> то
Х :^'*> то 
 . Тогда соответствующее нелинейное уравнение для z (t).эквивалентно, вообще говоря, нелинейной системе алгебраич. уравнений относительно коэффициентов a1, . .., a т. Функция z(t), вообще говоря, не однолистная при |t|<1, находится как решение этой алгебраич. системы уравнений. Класс однолистных в круге |t|<1 решений z(t), удовлетворяющих условиям z(0)=0, z'(0)>0, является решением поставленной П. т. о. з.
. Тогда соответствующее нелинейное уравнение для z (t).эквивалентно, вообще говоря, нелинейной системе алгебраич. уравнений относительно коэффициентов a1, . .., a т. Функция z(t), вообще говоря, не однолистная при |t|<1, находится как решение этой алгебраич. системы уравнений. Класс однолистных в круге |t|<1 решений z(t), удовлетворяющих условиям z(0)=0, z'(0)>0, является решением поставленной П. т. о. з.