|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОТЕНЦИАЛА ТЕОРИЯЗначение ПОТЕНЦИАЛА ТЕОРИЯ в математической энциклопедии: - в первоначальном понимании - учение о свойствах сил, действующих по закону всемирного тяготения. В формулировке этого закона, данной И. Ньютоном (I. Newton, 1687), речь идет только о силах взаимного притяжения, действующих на две материальные частицы малых размеров, или материальные точки, прямо пропорциональные произведению масс этих частиц и обратно пропорциональные квадрату расстояния между частицами. Поэтому первой и важнейшей с точки зрения небесной механики и геодезии задачей было изучение сил притяжения материальной точки ограниченным гладким материальным телом- сфероидом и, в частности, эллипсоидом (ибо многие небесные тела имеют именно эту форму). После первых частных достижений И. Ньютона и др. ученых основное значение здесь имели работы Ж. Лагранжа (J. Lagrange, 1773), А. Лежандра (A. Legendre, 1784-94) и П. Лапласа (P. Laplace, 1782-99). Ж. Лагранж установил, что поле сил тяготения, как говорят теперь,- потенциальное, и ввел функцию, к-рую позже Дж. Грин (G. Green, 1828) назвал потенциальной, а К. Гаусс (С. Gauss, 1840) - просто потенциалом. Ныне достижения этого первоначального периода обычно входят в курсы классич. небесной механики (см. также [2]). Еще К. Гаусс и его современники обнаружили, что потенциалов метод применим не только для решения задач теории тяготения, но и вообще для решения широкого круга задач математич. физики, в частности электростатики и магнетизма. В связи с этим стали рассматриваться потенциалы не только физически реальных в вопросах взаимного притяжения положительных масс, но и "масс" произвольного знака, или зарядов. В П. т. определились основные краевые задачи такие, как Дирихле задача и Неймана задача, электростатич. задача о статич. распределении нарядов на проводниках, или Робена задача, задача о выметании масс (см. Выметания метод). Для решения указанных задач в случае областей с достаточно гладкой границей оказались эффективным средством специальные разновидности потенциалов, т. е. специальные виды интегралов, зависящих от параметров, такие, как потенциал объемно распределенных масс, потенциалы простого и двойного слоя, логарифмич. потенциалы, потенциалы Грива и др. Основную роль в создании строгих методов решения основных краевых задач сыграли работы А. М. Ляпунова и В. А. Стеклова кон. 19 в. Изучение свойств потенциалов различных видов приобрело в П. т. и самостоятельное значение. Мощный стимул в направлении обобщения основных задач и законченности формулировок П. т. получила начиная с 1-й пол. 20 в. на основе использования общих понятий меры в смысле Радона, емкости и обобщенных функций. Современная П. т. тесно связана в своем развитии с теорией аналитич. ций, гармонич. функций, субгармонич. функций и теорией вероятностей. Наряду с дальнейшим углубленным изучением классических краевых задач и обратных задач (см. Потенциала теории обратные задачи).для современного периода развития П. т. характерно применение методов и понятий современной топологии и функционального анализа, применение абстрактных аксиоматич. методов (см. Потенциала теория абстрактная). Основные типы потенциалов и их свойства. Пусть S - гладкая замкнутая поверхность, то есть ( п-1)-мерное гладкое многообразие без края, в n-мерном евклидовом пространстве - главное фундаментальное решение уравнения Лапласа - расстояние между точками x=(x1, . . ., х п).и y=(y1 ,..., y п). в где n у - направление внешней относительно G+ нормали к Sв точке Производные 2-го порядка непрерывны всюду вне S, но при переходе через поверхность Sони претерпевают разрыв, причем в области G+ удовлетворяется уравнение Пуассона - Если G, - конечная область пространства R" с границей S1=дG1 класса С 1, то справедлива формула Гаусса для объемного потенциала: Пусть в частности, при n=2 тогда и только тогда, когда Потенциал простого слоя непрерывен всюду в где Через дV(x)/дnx здесь обозначено т. н. прямое значение нормальной производной потенциала простого слоя, вычисленное на поверхности S, то есть к-рое является непрерывной функцией точки Перечисленные свойства характеризуют потенциал простого слоя. Пусть При переходе через поверхность Sпотенциал двойного слоя испытывает скачок: где W+ (х).и W- (х) - предельные значения потенциала двойного слоя соответственно из G+ и G-, то есть Через W(х).при к-рое является непрерывной функцией точки Касательные производные потенциала двойного слоя также испытывают скачок при переходе через поверхность S, но нормальная производная дW(x)/dnx сохраняет свое значение при переходе через S: Перечисленные свойства характеризуют потенциал двойного слоя. В случае постоянной плотности v=1 имеет место формула Гаусса для потенциала двойного слоя: Интеграл в левой части этого равенства интерпретируется как (деленный на wn( п-2)) телесный угол, под к-рым видна поверхность Sиз точки х. Ниже дополнительно приводятся нек-рые свойства потенциалов при меньших ограничениях на плотности и поверхность S. Если где dij=1 при i=j, dij = 0 при Пусть Если Если Для доопределенных по непрерывности потенциалов и их производных на поверхности Sописанные выше свойства гладкости также остаются в силе при соответствующих условиях гладкости на плотность и поверхность S. Представление функций и решение основных краевых задач теории потенциала с помощью потенциалов. Пусть Ф (х) - функция класса В частности, в области G функция Ф(х).представима в виде суммы объемного потенциала и потенциалов простого и двойного слоя соответственно с плотностями Для гармонической в области Gфункции и(х).класса и поэтому такая функция и(х).представима в G в виде суммы потенциалов простого и двойного слоя соответственно с плотностями m(у)=ди (у)/дп у, v (у)=-и (у). Однако эти плотности в формуле (3) не могут задаваться произвольно на S, они связаны интегральным соотношением, получающимся из (3) при Центральное место в П. т. занимают краевые задачи Дирихле и Неймана (наз. также первой и второй краевыми задачами) для областей G+ (внутренние задачи) и G- (внешние задачи), к-рые в предположении достаточной гладкости поверхности удается полностью исследовать сведением их к интегральным уравнениям П. т. Внутренняя задача Дирихле: найти гармоническую в G+ функцию и(х).класса с плотностью v, к-рая находится как единственное решение интегрального уравнения Фредгольма 2-го рода Внутренняя задача Неймана: найти гармоническую в области G+ функцию и(х).класса Это решение определяется с точностью до произвольной аддитивной постоянной Св виде u(x)=V (х)+С, где - потенциал простого слоя, плотность m к-рого определяется из интегрального уравнения Фредгольма 2-го рода Соответствующее однородное уравнение имеет нетривиальное решение m0(x)> а неоднородное уравнение (5) разрешимо при выполнении условия (4), причем его общее решение имеет вид Внешняя задача Дирихле: найти гармоническую в области Решение этой задачи всегда существует, единственно и может быть найдено в виде где А - постоянная, - потенциал двойного слоя, плотность v к-рого является решением интегрального уравнения Фредгольма 2-го рода Соответствующее однородное уравнение имеет нетривиальное решение где плотность v0 должна удовлетворять условию Эта плотность v0 есть нетривиальное решение уравнения (5) внутренней задачи Неймана с данными y + (х)=0, Потенциал простого слоя V0(x).плотности v0(x) наз. равновесным потенциалом, или потенциалом Робена. Плотность v0(x) дает решение задачи Робена или электростатич. задачи о распределении зарядов на проводнике S, создающем равновесный потенциал, постоянный в области G+. Нек-рая сложность решения внешней задачи Дирихле происходит из-за того, что регулярная на бесконечности гармонич. функция и(х), вообще говоря, убывает при Внешняя задача Неймана: найти гармоническую в области причем решение определено лишь с точностью до произвольной аддитивной постоянной. Решение внешней задачи Неймана представимо в виде потенциала простого слоя плотность m к-poro есть решение интегрального уравнения Фредгольма 2-го рода При Решение краевых задач П. т. может быть получено также с помощью Грина функции. Напр., для (внутренней) задачи Дирихле функция Грина имеет вид где g(x, у) - гармонич. функция в G+ и непрерывная в Зависящие от параметра хинтегралы наз. соответственно объемным потенциалом Грина (задачи Дирихле), потенциалом Грина двойного слоя. Их свойства аналогичны свойствам потенциалов (1). С помощью функции Грина к интегральным уравнениям сводятся задачи на собственные значения. Напр., задача Дирихле Дальнейшее обобщение некоторых основных понятий теории потенциала. Параллельно с углубленным изучением свойств потенциалов (1), определяемых плотностями более пли менее общего вида, и их применений само понятие потенциала подверглось начиная примерно с 20-х гг. 20 в. глубокому обобщению, связанному с понятием меры и интеграла Радона. Пусть существует всюду в Rn в смысле отображения Потенциал (10) конечен, т. е. верхняя грань Еl(х).есть верхняя грань сужения Еlна supp l. Если это сужение непрерывно (в обобщенном смысле, включая значение Если Т - обобщенная функция, или распределение, в Для областей Поэтому важное значение имеет полученное в ходе развития метода Перрона обобщенное решение в смысле Перрона - Винера задачи Дирихле для уравнения Лапласа. Как показал Н. Винер (N. Wiener, 1924), при этом любая конечная непрерывная функция j=j+ , заданная на границе S=дG произвольной конечной области Обобщенное решение Hj (х).не во всех граничных точках принимает заданные значения j. Точка Прочие точки Для задачи Дирихле строится соответственно и обобщенная функция Грина G, к-рую можно определить, напр., для произвольно фиксированной точки Обобщенная функция Грина сохраняет нек-рые свойства классич. функции Грина, напр. свойство симметрии Важное значение имеют также исследования задачи Дирихле для компактов и устойчивости задачи Дирихле (см. [6], [4]). Интенсивно развивается изучение потенциалов с другими ядрами, отличными от ядра Е( х, у), и их применений для решения краевых задач (см. Бесселев потенциал. Нелинейный потенциал, Рисса потенциал, а также [3], [11]). Лит.:[1] Гюнтер Н. М., Теория потенциала и ее применение к основным задачам математической физики, М., 1953; [2] Сретенский Л. Н., Теория ньютоновского потенциала, М.- Л., 1946; [3] Ландкоф Н. С., Основы современной теории потенциала, М., 1966; [4] Брело М., Основы классической теории потенциала, пер. с франц., М., 1964; [5] Kellogg О. D., Foundations of potential theory, В., 1929; [6] Келдыш М. В., "Успехи матем. наук", 1941, в. 8, с. 171 - 231; [7] Бицадзе А. В., Уравнения математической физики, М., 1976; [8] его же. Краевые задачи для эллиптических уравнений второго порядка, М., 1966; 19] Владимиров В. С., Уравнения математической физики, 4 изд., М., 1981; [10] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [11] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М.. 1957; [12] Михлин С. Г., Линейные уравнения в частных производных, М., 1977; [13] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 5 изд., М., 1977. А. И. Прилепко, Е. Д. Соломенцев. |
|
|
|

 , ограничивающая конечную область G=G+ , дG=S, и пусть G-=
, ограничивающая конечную область G=G+ , дG=S, и пусть G-= - внешняя бесконечная область. Пусть
- внешняя бесконечная область. Пусть 
 в
в  , где
, где 
 ,
,  - площадь единичной сферы в
- площадь единичной сферы в  , Г - гамма-функция. Три интеграла, зависящих от хкак от параметра:
, Г - гамма-функция. Три интеграла, зависящих от хкак от параметра: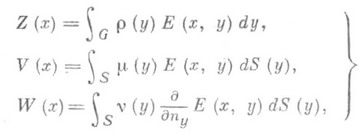 (1)
(1) , наз. соответственно объемным потенциалом, потенциалом простого слоя и потенциалом двойного слоя. Функции r(у),m(y).и v(y).наз. плотностями соответствующих потенциалов; ниже они будут предполагаться абсолютно интегрируемыми соответственно на Gили S. При n=3 (а иногда и при п
, наз. соответственно объемным потенциалом, потенциалом простого слоя и потенциалом двойного слоя. Функции r(у),m(y).и v(y).наз. плотностями соответствующих потенциалов; ниже они будут предполагаться абсолютно интегрируемыми соответственно на Gили S. При n=3 (а иногда и при п  3) интегралы (1) наз. ньютоновым объемным потенциалом, ньютоновыми потенциалами простого и двойного слоя, при n=2 - логарифмическими потенциалами масс, простого и двойного слоя. Пусть r принадлежит классу
3) интегралы (1) наз. ньютоновым объемным потенциалом, ньютоновыми потенциалами простого и двойного слоя, при n=2 - логарифмическими потенциалами масс, простого и двойного слоя. Пусть r принадлежит классу 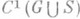 . Тогда объемный потенциал и его производные 1-го порядка непрерывны всюду в
. Тогда объемный потенциал и его производные 1-го порядка непрерывны всюду в  , причем их можно вычислить посредством дифференцирования под знаком интеграла, то есть
, причем их можно вычислить посредством дифференцирования под знаком интеграла, то есть  . Далее,
. Далее,
 , а в G-- уравнение Лапласа
, а в G-- уравнение Лапласа  . Перечисленные свойства характеризуют объемный потенциал.
. Перечисленные свойства характеризуют объемный потенциал.
 . Потенциал простого слоя V(х).есть гармонич. функция при
. Потенциал простого слоя V(х).есть гармонич. функция при  , причем
, причем 
 при n
при n 3, но
3, но 

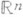 ,
,  , причем V(х).и его касательные производные непрерывны при переходе через поверхность S. Нормальная производная потенциала простого слоя при переходе через поверхность Sиспытывает скачок:
, причем V(х).и его касательные производные непрерывны при переходе через поверхность S. Нормальная производная потенциала простого слоя при переходе через поверхность Sиспытывает скачок:
 и
и  - предельные значения нормальной производной соответственно из G+ и G-, то есть
- предельные значения нормальной производной соответственно из G+ и G-, то есть 

 , а ядро дЕ( х, у)/дп х имеет слабую особенность на S,
, а ядро дЕ( х, у)/дп х имеет слабую особенность на S,
 . Потенциал двойного слоя W(x).есть гармонич. функция при
. Потенциал двойного слоя W(x).есть гармонич. функция при  , причем
, причем 


 обозначено т. н. прямое значение потенциала двойного слоя, вычисленное на поверхности S, то есть
обозначено т. н. прямое значение потенциала двойного слоя, вычисленное на поверхности S, то есть 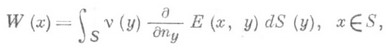
 , а ядро дЕ( х, у)/дп у имеет слабую особенность на S.
, а ядро дЕ( х, у)/дп у имеет слабую особенность на S.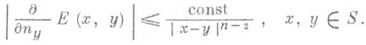


 , то Z(x) - гармонич. функция при
, то Z(x) - гармонич. функция при  и Z(x).суммируема в G+ . Если r
и Z(x).суммируема в G+ . Если r Lp(G), 1
Lp(G), 1 p
p n/2, то Z
n/2, то Z Lq(
Lq( ), l/p+l/q=l, 1<q<np/(n-2p);если r
), l/p+l/q=l, 1<q<np/(n-2p);если r Lp(G), p>n/2, тоZ
Lp(G), p>n/2, тоZ C(Rn). Если r
C(Rn). Если r Lp(G), 1
Lp(G), 1 р
р  n, то Z
n, то Z (
( ), 1<q<np/(n-р);если r
), 1<q<np/(n-р);если r Lp(G), p>n, то Z
Lp(G), p>n, то Z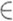 G1(
G1( ). Если r
). Если r L2(G), то существуют обобщенные производные 2-го порядка от Z(х), они также принадлежат классу L2(G).и выражаются с помощью сингулярных интегралов:
L2(G), то существуют обобщенные производные 2-го порядка от Z(х), они также принадлежат классу L2(G).и выражаются с помощью сингулярных интегралов:
 ; если r
; если r Lp(G), 1<р<
Lp(G), 1<р< , то все обобщенные производные д 2Z/dxidxj также существуют и принадлежат
, то все обобщенные производные д 2Z/dxidxj также существуют и принадлежат  . Если р
. Если р  Lp(G),
Lp(G), , то Z(x).есть обобщенное решение уравнения Пуассона -DZ=r(х),
, то Z(x).есть обобщенное решение уравнения Пуассона -DZ=r(х),  . Если r
. Если r С (1,a)(G) и S
С (1,a)(G) и S С (0,a), 0<a<1, то Z
С (0,a), 0<a<1, то Z С (2,a) в G+ или G-. Если r
С (2,a) в G+ или G-. Если r С (l,a)(G) и S
С (l,a)(G) и S С (k+1,a), 0<a<1, l, k- целые,
С (k+1,a), 0<a<1, l, k- целые,  , то Z
, то Z С(l+2,a)(G+).
С(l+2,a)(G+). - замкнутая конечная область такая, что
- замкнутая конечная область такая, что  . Тогда если
. Тогда если  , дV/dxi
, дV/dxi Lp(D),p=l, 2; i=l, 2, ..., n. Если плотность m ограниченная и суммируемая, то
Lp(D),p=l, 2; i=l, 2, ..., n. Если плотность m ограниченная и суммируемая, то 
 в G+ или G-. Если
в G+ или G-. Если  в G + или G-.
в G + или G-. - целые,
- целые,  , то
, то  в G+ или G-. Если v
в G+ или G-. Если v C(l,a)(S) и S
C(l,a)(S) и S C(k+1,a), 0<a<1, l, k - целые,
C(k+1,a), 0<a<1, l, k - целые,  , то W
, то W C(l,a) в G+ или G-.
C(l,a) в G+ или G-. - гладкая поверхность класса С 2. Тогда справедливо интегральное тождество (формула Грина):
- гладкая поверхность класса С 2. Тогда справедливо интегральное тождество (формула Грина): (2)
(2)
 имеет место тождество
имеет место тождество  , (3)
, (3) .
. ,
,  , удовлетворяющую краевому условию u(x).j+(x),
, удовлетворяющую краевому условию u(x).j+(x), , где j+ (х) - данная непрерывная функция на S. Решение этой задачи всегда существует, единственно и может быть найдено в виде потенциала двойного слоя
, где j+ (х) - данная непрерывная функция на S. Решение этой задачи всегда существует, единственно и может быть найдено в виде потенциала двойного слоя 

 , удовлетворяющую краевому условию
, удовлетворяющую краевому условию  , где y+ (х) - данная непрерывная функция на S. Решение этой задачи существует тогда и только тогда, когда функция y+(x). удовлетворяет условию ортогональности
, где y+ (х) - данная непрерывная функция на S. Решение этой задачи существует тогда и только тогда, когда функция y+(x). удовлетворяет условию ортогональности  (4)
(4)
 (5)
(5) , где с - произвольная постоянная.
, где с - произвольная постоянная.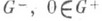 , функцию u(х).класса
, функцию u(х).класса  , удовлетворяющую краевому условию
, удовлетворяющую краевому условию  , где j-(x) - данная непрерывная функция на S;при этом и(х).предполагается регулярной на бесконечности, т. е.
, где j-(x) - данная непрерывная функция на S;при этом и(х).предполагается регулярной на бесконечности, т. е.


 (6)
(6) . При надлежащем выборе постоянной Арешение неоднородного уравнения (6) имеет вид
. При надлежащем выборе постоянной Арешение неоднородного уравнения (6) имеет вид 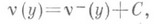 где С - произвольная постоянная, a v-(y) - частное решение ур-ния (6). Постоянная Аподбирается в виде
где С - произвольная постоянная, a v-(y) - частное решение ур-ния (6). Постоянная Аподбирается в виде 
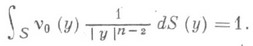 (7)
(7) , удовлетворяющее эквивалентному (7) при
, удовлетворяющее эквивалентному (7) при  условию нормировки
условию нормировки 
 медленнее, чем потенциал двойного слоя, и поэтому u(x) в общем случае нельзя представить в виде одного только потенциала двойного слоя.
медленнее, чем потенциал двойного слоя, и поэтому u(x) в общем случае нельзя представить в виде одного только потенциала двойного слоя. , функцию и(x) класса
, функцию и(x) класса  , удовлетворяющую краевому условию
, удовлетворяющую краевому условию  , где y- (х) - данная непрерывная функция на S;при этом и(х).предполагается регулярной на бесконечности. При
, где y- (х) - данная непрерывная функция на S;при этом и(х).предполагается регулярной на бесконечности. При  решение этой задачи всегда существует и единственно; при п=2 решение существует тогда и только тогда, когда выполняется условие
решение этой задачи всегда существует и единственно; при п=2 решение существует тогда и только тогда, когда выполняется условие  (8)
(8)
 (9)
(9) решение этого уравнения всегда существует и единственно. При n=2 соответствующее однородное уравнение имеет нетривиальное решение m0(x), поэтому неоднородное уравнение (9) при выполнении условия разрешимости (8) имеет единственное решение
решение этого уравнения всегда существует и единственно. При n=2 соответствующее однородное уравнение имеет нетривиальное решение m0(x), поэтому неоднородное уравнение (9) при выполнении условия разрешимости (8) имеет единственное решение  такое, что
такое, что  а его общее решение имеет вид
а его общее решение имеет вид  , где с- произвольная постоянная.
, где с- произвольная постоянная.
 но x, для каждого
но x, для каждого  удовлетворяющая краевому условию
удовлетворяющая краевому условию  . Решение (внутренней) задачи Дирихле и(х).класса
. Решение (внутренней) задачи Дирихле и(х).класса  для уравнения Пуассона
для уравнения Пуассона  , с краевым условием
, с краевым условием  , представимо в виде
, представимо в виде 

 , с краевым условием
, с краевым условием  , сводится к интегральному уравнению Фредгольма 2-го рода с самосопряженным ядром
, сводится к интегральному уравнению Фредгольма 2-го рода с самосопряженным ядром 
 - положительная борелевская мера на пространстве
- положительная борелевская мера на пространстве  с компактным носителем supp l. Потенциал меры
с компактным носителем supp l. Потенциал меры  (10)
(10)
 при
при  и
и  при n=2 (т. е. здесь допускается и значение
при n=2 (т. е. здесь допускается и значение  ) и является супергармонической функцией всюду в
) и является супергармонической функцией всюду в  , гармонической - вне носителя меры supp l. Для меры l. произвольного знака с компактным носителем потенциал El определяется, исходя из канонич. разложения l
, гармонической - вне носителя меры supp l. Для меры l. произвольного знака с компактным носителем потенциал El определяется, исходя из канонич. разложения l , в виде
, в виде  . В тех точках
. В тех точках  , где оба потенциала Еl+ (х). и Еl- (х). принимают значение
, где оба потенциала Еl+ (х). и Еl- (х). принимают значение  , этот потенциал не определен. Если мера
, этот потенциал не определен. Если мера  сосредоточена на гладкой поверхности S, то аналогично (10) определяется и потенциал двойного слоя меры l:
сосредоточена на гладкой поверхности S, то аналогично (10) определяется и потенциал двойного слоя меры l:
 , всюду в
, всюду в  , за исключением точек полярного множества, к-рое характеризуется как множество внешней емкости нуль. Если Еl(х)=0 всюду, кроме множества внешней емкости нуль, то l=0. Если мера
, за исключением точек полярного множества, к-рое характеризуется как множество внешней емкости нуль. Если Еl(х)=0 всюду, кроме множества внешней емкости нуль, то l=0. Если мера  сосредоточена на множестве емкости нуль, то sup
сосредоточена на множестве емкости нуль, то sup  . Справедлив следующий принцип максимума:
. Справедлив следующий принцип максимума:
 ) в точке х 0
) в точке х 0 supp l, то потенциал Еl(х).непрерывен в точке х 0 в
supp l, то потенциал Еl(х).непрерывен в точке х 0 в  . Потенциалы мер Еlсводятся к потенциалам плотностей (1) тогда и только тогда, когда мера l абсолютно непрерывна по мере Лебега соответственно на Gили на S(см. [3]-[6]).
. Потенциалы мер Еlсводятся к потенциалам плотностей (1) тогда и только тогда, когда мера l абсолютно непрерывна по мере Лебега соответственно на Gили на S(см. [3]-[6]). , то потенциал распределения определяется как свертка Е*Т, являющаяся также обобщенной функцией. Напр., если Т - финитная обобщенная функция, то в
, то потенциал распределения определяется как свертка Е*Т, являющаяся также обобщенной функцией. Напр., если Т - финитная обобщенная функция, то в  в смысле обобщенных функций справедливо уравнение Пуассона
в смысле обобщенных функций справедливо уравнение Пуассона  Потенциалы мер можно рассматривать как частный случай потенциалов распределений. О потенциалах распределений см. [3], [4], [9].
Потенциалы мер можно рассматривать как частный случай потенциалов распределений. О потенциалах распределений см. [3], [4], [9]. с достаточно гладкой границей Sметод потенциалов дает эффективное решение задачи Дирихле. Одно из основных направлений развития П. т. состоит в открытии методов доказательства существования и единственности решения задачи Дирихле для все более широких классов областей (см. Выметания метод, Дирихле принцип, Перрона метод, Шварца альтернирующий метод). Однако в 1910 С. Заремба (S. Zaremba) заметил, что для плоской области Gпри наличии изолированных точек границы дG=S задача Дирихле в приведенной выше классич. постановке не всегда разрешима; более того, в 1912 А. Лебег (Н. Lebesgue) показал, что она не всегда разрешима и для пространственных областей, гомеоморфных шару, при наличии достаточно острого входящего в область острия границы (т. н. острие Лебега, см. Иррегулярная граничная точка), т. е. существуют такие непрерывные функции
с достаточно гладкой границей Sметод потенциалов дает эффективное решение задачи Дирихле. Одно из основных направлений развития П. т. состоит в открытии методов доказательства существования и единственности решения задачи Дирихле для все более широких классов областей (см. Выметания метод, Дирихле принцип, Перрона метод, Шварца альтернирующий метод). Однако в 1910 С. Заремба (S. Zaremba) заметил, что для плоской области Gпри наличии изолированных точек границы дG=S задача Дирихле в приведенной выше классич. постановке не всегда разрешима; более того, в 1912 А. Лебег (Н. Lebesgue) показал, что она не всегда разрешима и для пространственных областей, гомеоморфных шару, при наличии достаточно острого входящего в область острия границы (т. н. острие Лебега, см. Иррегулярная граничная точка), т. е. существуют такие непрерывные функции  , для к-рых задача Дирихле не разрешима никаким способом.
, для к-рых задача Дирихле не разрешима никаким способом. , разрешима, т. е. для нее существует и притом единственное обобщенное решение Hj (х).в смысле Перрона - Винера. Вообще, в 1939 М. Брело (М. Brelot) показал, что конечная измеримая функция j на Sразрешима тогда и только тогда, когда j интегрируема по гармонической мере на S.
, разрешима, т. е. для нее существует и притом единственное обобщенное решение Hj (х).в смысле Перрона - Винера. Вообще, в 1939 М. Брело (М. Brelot) показал, что конечная измеримая функция j на Sразрешима тогда и только тогда, когда j интегрируема по гармонической мере на S. наз. регулярной, если для любой конечной непрерывной функции j на Sобобщенное решение Hj (х). црини-мает значение j(x0), то есть
наз. регулярной, если для любой конечной непрерывной функции j на Sобобщенное решение Hj (х). црини-мает значение j(x0), то есть 
 наз. иррегулярными, к ним относятся изолированные точки границы при
наз. иррегулярными, к ним относятся изолированные точки границы при  и острие Лебега при
и острие Лебега при  . Как оказалось ( Келлога - Эванса теорема,1933), множество иррегулярных точек имеет внешнюю емкость нуль, т. е. является в нек-ром смысле разреженным. Множество регулярных точек плотно на S.
. Как оказалось ( Келлога - Эванса теорема,1933), множество иррегулярных точек имеет внешнюю емкость нуль, т. е. является в нек-ром смысле разреженным. Множество регулярных точек плотно на S. следующим образом:
следующим образом:
 , тогда и только тогда, когда x0 - регулярная точка границы S(см. [4], [6]).
, тогда и только тогда, когда x0 - регулярная точка границы S(см. [4], [6]).