|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОШИБОЧНОГО ДЕКОДИРОВАНИЯ ВЕРОЯТНОСТЬЗначение ОШИБОЧНОГО ДЕКОДИРОВАНИЯ ВЕРОЯТНОСТЬ в математической энциклопедии: - одна из возможных мер характеризации точности воспроизведения сообщений, передаваемых по каналу связи (см. также Сообщений точность воспроизведения). Пусть для передачи сообщения x, вырабатываемого источником сообщений и принимающего Мразличных возможных значений 1,. . ., М с распределением вероятностей р m=Р{x=m}, m=l, , . . , M, используется нек-рый канал связи. Тогда для фиксированных методов кодирования и декодирования (см. также Информации передача).О. д. в. Р е, т, m=1, . . ., М, определяется равенством где Особый интерес представляет изучение оптимальной О. д. в. где нижняя грань берется по всевозможным методам кодирования и декодирования. Ввиду трудностей получения точного выражения для где a(N) и b(N).стремятся к нулю с ростом N,aфункции Er(R).и Esp(R).определяются следующим образом: Здесь
Для значении Лит.:[1] Галлагер Р., Теория информации и надежная связь, пер. с англ., М., 1974; 12] Файнстейн А., Основы теории информации, пер. о англ., М., I960. Р. Л. Добрушин, В. В. Прелов. НАДЕ АППРОКСИМАЦИЯ - наилучшая рациональная аппроксимация степенного ряда. Пусть - произвольный степенной ряд (формальный или сходящийся), где s(j) - индекс первого из отличных от нуля коэффициентов ряда
Функцию p п, т можно определить также как отношение p п, т=p/qлюбых многочленов При фиксированных п, т существует единственная П. а. p п, т ряда (1). Таблица Вычисление функции p п, т сводится к решению системы линейных уравнений, коэффициенты к-рых выражаются через коэффициенты fk, k=0, l,. . ., n+m, заданного ряда. Если отличен от нуля определитель Ганкеля то знаменатель q п, т функции p п, т определяется по формуле (нормировка q п, т(0)=1; явная формула может быть написана и для числителя функции p п, т). При этом Последнее соотношение иногда принимают за определение П. а.; в этом случае П. а. могут не существовать для нек-рых (n, т). Для обозначения П. а. типа ( п, т).заданного ряда f часто употребляется символ [n/m] = [n/m]f. Для эффективного вычисления П. а. удобнее пользоваться не явными формулами, а рекурентными соотношениями, существующими в таблице Паде. Разработано большое количество алгоритмов для машинного вычисления П. а.; эти вопросы имеют особенно важное значение в связи с приложениями (см. [17], [18]). Впервые общую задачу об интерполяции заданных значений функции в n+m+1 различных точках посредством рациональной функции класса R п, т рассмотрел О. Коши [1]; К. Якоби [2] распространил результаты О. Коши на случай кратных узлов интерполяции. Случай одного (n+m+1 )-кратного узла интерполяции соответствует П. а. Понятие П. а. сформировалось в кон. 19 в. в рамках классич. теории непрерывных дробей (Г. Фробениус [3], А. Паде [4]). Фундаментальные результаты о диагональных П. а. были получены П. Л. Чебышевым, А. А. Марковым, Т. Стильтьесом (Т. Stieltjes) в терминах непрерывных дробей; ими были обнаружены и исследованы связи диагональных П. а. с ортогональными многочленами, квадратурными формулами, проблемой моментов и другими вопросами классич. анализа (см. [7] - [9]). Начало изучению строк таблицы Паде было положено работами о радиусах мероморфности функции, заданной степенным рядом, и о сходимости строк таблицы Паде в кругах мероморфности (см. [5], [6]). С нач. 20 в. П. а. становятся самостоятельным объектом анализа и составляют важную главу теории рациональных приближений аналитич. ций. Используя для своего построения локальные данные (коэффициенты степенного ряда), они позволяют изучать глобальные свойства соответствующей аналитич. ции (аналитич. продолжение, характер и расположение особенностей и т. п.) и вычислять значение функции за пределами круга сходимости степенного ряда. Наряду с классическими П. а. рассматриваются различные их обобщения: общие процессы интерполяции посредством рациональных функций со свободными полюсами (многоточечные аппроксимации Паде); рациональные аппроксимации рядов по заданной системе многочленов (напр., по ортогональным многочленам); совместные П. а. (аппроксимации Паде - Эрмита); рациональные аппроксимации (типа П. а.) степенных рядов от нескольких переменных и др. Лит.:[1] Саuсhу A.-L., Cours d'analyse de I'Ecole royale polyteclmique, pt. 1- Analyse algebrique, P., 1821; [2] Jacobi C. G. J., "J. reine und angew. Math.", 1846, Bd SO, S. 127-56; [3] Frоbenius G., там же, 1881, Bd 90, S. 1 - 17; [4] Pade H., "Ann. scient. Ecole norm, super.", 1892, t. 9, p. 1-93; [5] Hadamard J., "J. math, pures et appl.", 1892, t. 8, p. 101-86; [6] Mоntessus deBalloreB.de, "Bull. Soc. math. France", 1902, t. 3(1, p. 28-36; [7] Чебышев П. Л., Полн. собр. соч., т. 3, М.- Л., 1948; [8] Марков А. А., Избр. труды по теории непрерывных дробей и теории функций, наименее уклоняющихся от нуля, М.- Л., 1948; [9] Стилтьес Т., Исследования о непрерывных дробях, пер. с франц., Хар.- К.. 1936; [10] Wall H. S., Analytic theory of continued fractions, Toronto - N. Y,- L., 1948; [11] Perron O., Die Lehre von den Kettenbruchen, 3 Aufl., Bd 2, Stuttg., 1957; [12] The Fade approximant in theoretical physics, N. Y.- L., 1970; [13] Pade approximants and their applications, L.-N. Y., 1973; [14] Pade approximants method and its applications to mechanics, В.- Hdlb.- N. Y., 1976; [15] В a k e r G. A., Essentials of Fade approximants, N. Y.- San Franc.- L., 1975; [16] Fade and rational approximation, N. Y.- [a. o.], 1977; [17] Gilewicz J., Approximants dc Pade, В.- Hdlb.- N. Y., 1978; [18] Pade approximation and its applications, В.- Hdlb.- N. Y., 1979. В. А. Рахманов. |
|
|
|


 - декодированное сообщение на выходе канала. Средней О. д. в. Р е наз. величина
- декодированное сообщение на выходе канала. Средней О. д. в. Р е наз. величина 
 , определяемой равенством
, определяемой равенством 
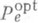 , связанных с тем обстоятельством, что в общем случае неизвестны оптимальные методы кодирования, интерес представляет изучение асимптотич. поведения
, связанных с тем обстоятельством, что в общем случае неизвестны оптимальные методы кодирования, интерес представляет изучение асимптотич. поведения  при возрастании длительности передачи по каналу. Точнее, рассматривается следующая ситуация. Пусть для передачи используется отрезок длины N канала связи с дискретным временем и R=(ln M)/N. Требуется изучить асимптотич. поведение
при возрастании длительности передачи по каналу. Точнее, рассматривается следующая ситуация. Пусть для передачи используется отрезок длины N канала связи с дискретным временем и R=(ln M)/N. Требуется изучить асимптотич. поведение  при
при  и R=const (это означает, что длительность передачи возрастает, а ее скорость остается постоянной). Если рассматриваемый отрезок канала является отрезком однородного канала без памяти с дискретным временем и конечными пространствами Y и
и R=const (это означает, что длительность передачи возрастает, а ее скорость остается постоянной). Если рассматриваемый отрезок канала является отрезком однородного канала без памяти с дискретным временем и конечными пространствами Y и  значений компонент сигналов на входе и выходе, то известны следующие верхние и нижние оценки
значений компонент сигналов на входе и выходе, то известны следующие верхние и нижние оценки  :
: (1)
(1)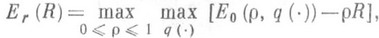 (2)
(2) (3) где
(3) где 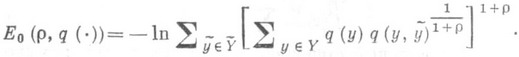
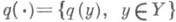 - произвольное распределение вероятностей на
- произвольное распределение вероятностей на  ,
, ,- компоненты сигналов на входе и выходе рассматриваемого канала без памяти. Известно, что Er(R).и Esp,(R), определяемые формулами (2) и (3), являются положительными, выпуклыми вниз, монотонно убывающими функциями от Rпри
,- компоненты сигналов на входе и выходе рассматриваемого канала без памяти. Известно, что Er(R).и Esp,(R), определяемые формулами (2) и (3), являются положительными, выпуклыми вниз, монотонно убывающими функциями от Rпри 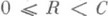 , где С - канала пропускная способность, причем Er(R)=Esp(R). при
, где С - канала пропускная способность, причем Er(R)=Esp(R). при  , здесь Rcr - величина, определяемая переходной матрицей канала и называемая критической скоростью для данного канала без памяти. Таким образом, для значений
, здесь Rcr - величина, определяемая переходной матрицей канала и называемая критической скоростью для данного канала без памяти. Таким образом, для значений 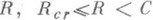 , главные члены верхней и нижней оценок (1) для
, главные члены верхней и нижней оценок (1) для  асимптотически совпадают, откуда следует, что для этого диапазона изменения Rизвестно точное значение функции надежности канала Е(R), определяемой равенством
асимптотически совпадают, откуда следует, что для этого диапазона изменения Rизвестно точное значение функции надежности канала Е(R), определяемой равенством 
 , точное значение E(R).для произвольных каналов без памяти неизвестно (1983), хотя оценки (1) и могут быть улучшены. Экспоненциальный характер убывания
, точное значение E(R).для произвольных каналов без памяти неизвестно (1983), хотя оценки (1) и могут быть улучшены. Экспоненциальный характер убывания 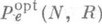 доказан для весьма широкого класса каналов.
доказан для весьма широкого класса каналов.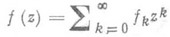 (1)
(1)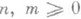 - целые числа, R п, т - класс всех, рациональных функций вида р/q, где ри q - многочлены от
- целые числа, R п, т - класс всех, рациональных функций вида р/q, где ри q - многочлены от 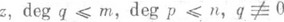 . Аппроксимацией Паде типа ( п, т).ряда (1) (функции f) наз. рациональная функция
. Аппроксимацией Паде типа ( п, т).ряда (1) (функции f) наз. рациональная функция  , имеющая максимально возможный в классе Rn,m порядок касания с рядом (1) в точке z=0. Точнее, функция p п, т определяется условием
, имеющая максимально возможный в классе Rn,m порядок касания с рядом (1) в точке z=0. Точнее, функция p п, т определяется условием 

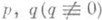 , удовлетворяющих соотношениям
, удовлетворяющих соотношениям  (2)
(2)  наз. таблицей Паде ряда (1). Последовательности вида
наз. таблицей Паде ряда (1). Последовательности вида 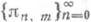 наз. строками таблицы Паде (нулевая строка совпадает с последовательностью многочленов Тейлора для f);
наз. строками таблицы Паде (нулевая строка совпадает с последовательностью многочленов Тейлора для f); 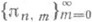 - столбцами таблицы Паде;
- столбцами таблицы Паде; 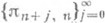 - диагоналями таблицы Паде. Наиболее важный частный случай f=0 - главная диагональ.
- диагоналями таблицы Паде. Наиболее важный частный случай f=0 - главная диагональ.