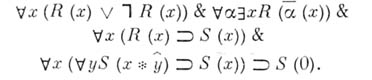БАР-ИНДУКЦИЯ

Значение БАР-ИНДУКЦИЯ в математической энциклопедии:

- индуктивный способ рассуждения, используемый в интуиционистской математике (см. Интуиционизм). и состоящий в следующем. Пусть на конечных кортежах натуральных чисел заданы нек-рые свойства такие, что: 1) свойство Rразрешимо, т. е. для всякого кортежа эффективно выясняется, выполнено Rна этом кортеже или нет; 2) для всякой свободно становящейся последовательности найдется кортеж вида , для к-рого выполнено R. При этом, если выполняется 2), то говорят, что R "запирает" пустой кортеж (отсюда и назв. "Б.-и.", "bar" - "запирать", "замок"); 3) для всякого кортежа л натуральных чисел, если - так наз. базис Б.-и.; 4) если - кортеж такой, что для всякого натурального kимеет место , то необходимо это свойство наз. шагом Б.-и.

Если выполняются перечисленные условия 1) - 4), то принцип Б.-и. позволяет заключить, что имеет место

Л. Э. Я. Брауэр (L. Е. J. Brouwer) предложил Б.-и. как интуиционистски приемлемый способ рассуждения, указывающий на незавершенность, нек-рую эффективную несчетность совокупности всех свободно становящихся последовательностей. В частности, было показано [С. К. Клпни (S. С. Kleene) и независимо А. А. Марковым], что из принципа Б.-и. (фактически даже из нек-рого следствия Б.-и. теоремы о веере).следует, что не все свободно становящиеся последовательности рекурсивны.

С 60-х гг. 20 в. в основаниях математики нашли употребление формы Б.-и., рассматривающие не кортежи натуральных чисел, а кортежи более сложных объектов, напр, кортежи свободно становящихся последовательностей.

На языке формального интуиционистского математич. анализа Б.-и. может быть записана в виде:

Лит.:[1] К1ееnе S. С., Yes ley R. E., The foundations of intuitionistic mathematics, Amst., 1965.

А. Г. Драгалин.