|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИНТУИЦИОНИЗМЗначение ИНТУИЦИОНИЗМ в математической энциклопедии: - совокупность философских и математич. идей и методов, рассматривающих математику как науку об умственных построениях. С точки зрения И., основным критерием истинности математич. суждения является интуитивная убедительность возможности построения мысленного эксперимента, связываемого с этим суждением. Поэтому в интуиционистской математике отвергается теоретико-множественный подход к определению математич. понятий, а также нек-рые способы рассуждения, принятые в классич. логике. Истоки И. можно проследить еще в античной математике, а позднее в высказываниях таких ученых, как К. Гаусс (С. Gauss), Л. Кронекер (L. Kronecker), А. Пуанкаре (Н. Poincare), А. Лебег (Н. Lebesgue), Э. Борель (Е. Borel). Начиная с 1904 в ряде статей выступил с развернутой критикой нек-рых концепций классич. математики Л. Э. Я. Брауэр (L. E. J. Вrоuwer). В основе этой критики лежит обсуждение статуса существования в математике: в каком смысле следует считать установленным существование актуально заданного бесконечного множества и могут ли быть построены в виде потенциально осуществимой конструкции такие объекты исследования, как неизмеримое множество действительных чисел, нигде не дифференцируемая функция? Естественно предположить, что можно построить произвольное натуральное число в виде последовательного ряда однородных предметов, напр. ряда параллельных черточек. В рамках такой же идеализации можно допустить, что, построив нек-рое натуральное число, можно построить затем и следующее добавив к уже построенному еще одну черточку. Но, возникает вопрос о том, с какого рода построением связано множество всех действительных чисел или множество всех натуральных чисел как единый объект исследования. Современные физич. воззрения также как будто не дают оснований полагать, что в окружающем нас мире актуально существуют бесконечные множества объектов. Есть серьезные основания считать, что объекты, существевание к-рых устанавливается без использования абстракции актуальной бесконечности, а лишь в рамках гораздо более скромной абстракции потенциальной осуществимости, имеют более непосредственное отношение к реальной действительности. Однако при обычной теоретико-множественной трактовке не делается никакого различия между объектами, существование к-рых можно подтвердить с помощью нек-рого потенциально осуществимого построения, и абстрактными теоретико-множественными объектами исследования. Способы установления свойств обоих типов объектов в классич. математике основаны на законах логики, возникших в результате экстраполяции законов, верных для конечных совокупностей, на бесконечные множества. В области бесконечного эти законы не ориентированы на эффективное построение объектов, существование к-рых утверждается. Фактически такое положение дел приводит к появлению в математике так наз. "теорем чистого существования", в к-рых утверждается существование нек-рых объектов и в то же время не указывается никакого способа отыскания этих объектов. Такова, напр., известная теорема классич. анализа, утверждающая, что всякая непрерывная действительная функция, заданная на замкнутом ограниченном множестве, имеет максимум. Обычное доказательство этой теоремы не дает никаких указаний на метод построения искомого максимума. Это обстоятельство может и не смущать теоретико-множественно настроенного математика: он может считать, что максимум "есть" у всякой функции рассматриваемого класса, независимо от того, можно его отыскать в каждом частном случае или нет, "есть" как объект нек-рого воображаемого мира ("платонистского мира", см. [6], с. 399). Однако такой подход не удовлетворяет, если принять во внимание возможности субъекта-иеследователя. Имеется ли способ отыскания максимума, и если этот способ не указан, то в каком смысле верно, что максимум существует у всякой функции рассматриваемого класса? Известно, сколь трудной является задача поиска экстремума у функций даже весьма узкого класса (многочлены с рациональными коэффициентами от нескольких переменных), и, что существенно, указанная теорема нисколько не помогает в решении этой задачи. Заметим, что описанная выше критика классич. математики не связана непосредственно с антиномиями теории множеств. Появление антиномий можно рассматривать как дополнительный довод в пользу неудовлетворительности теоретико-множественного подхода, но критика относится и к таким разделам математики, где антиномий, не возникает. Описанная критика теоретико-множественного подхода к математике исторически привела к возникновению двух путей преодоления трудностей в обосновании математики - интуиционизма Л. Э. Я. Брауэра и формализма Д. Гильберта (D. Hilbert). Обе концепции, развиваясь, оказывают в настоящее время (1970-е гг.) значительное влияние друг на друга. Так, при обосновании непротиворечивости формальных теорий необходимо уточнить приемы содержательных умозаключений в метаматематике, что делается обычно в рамках тех или иных интуиционистских концепций. С другой стороны, именно с помощью формализации метода удалось получить ряд важнейших результатов о логике интуиционизма. Интуиционистская математика есть наука об интуитивно убедительных мысленных построениях. Сам Л. Э. Я. Брауэр трактовал эту интуитивную убедительность идеалистически, рассматривая мысленные построения как таковые "безотносительно к таким вопросам о природе конструируемых объектов, как вопрос, существуют ли эти объекты независимо от нашего знания о них" (см. [1]). Однако возможно и материалистич. толкование "интуиции" И. как наглядной умственной убедительности простейших конструктивных процессов реальной действительности. И независимо от философских установок, конкретные математич. результаты, относящиеся к интуиционистской математике и логике, представляют большую научную ценность. При построении интуиционистской математики обычные логич. связки, употребляемые для формулировки математич. суждений, истолковываются способом, отличным от классического. Суждение считается истинным, только если исследователь имеет возможность его доказать. Доказательство же всегда связано с построением нек-рой мысленной конструкции. Так, утверждение, начинающееся с квантора существования E хА (х), может быть доказано только путем построения объекта х, для к-рого доказывается суждение (х). Дизъюнкция Объектами исследования интуиционистской математики являются прежде всего конструктивные объекты, такие, как натуральные числа, рациональные числа, конечные множества конструктивных объектов, заданные списком своих элементов. Своеобразным объектом исследования являются так наз. свободно становящиеся последовательности (с. с. п.; в другой терминологии - последовательности выбора). С. с. п. можно представлять себе как функцию, определенную на натуральном ряде, принимающую в качестве значений объекты исследования некоторого класса (в простейшем случае - натуральные числа) и такую, что всякое ее значение эффективно становится доступным исследователю. Точный анализ показывает, что следует различать несколько видов с. с. п. в зависимости от степени информации, известной исследователю относительно с. с. п. Так, если полностью известен закон образования с. с. п., напр, в виде записи соответствующего алгоритма, то такую с. с. п. наз. заданной законом. Другой крайний случай имеет место, если в каждый момент времени исследователю известен лишь нек-рый начальный отрезок с. с. п. и нет никакой информации относительно ее дальнейшего поведения; такие с. с. п. наз. беззаконными. Эти различия, игнорируемые в классич. математике, в интуиционистской математике могут быть отражены посредством точных математич. принципов, свидетельствующих о разных способах обращения с такими с. с. п. Наконец, объектами исследования интуиционистской математики могут быть и так наз. интуиционистские виды. Вид - свойство, к-рым, могут обладать объекты исследования. Объекты, удовлетворяющие этому свойству, наз. элементами вида, или его членами. Во избежание появления антиномий среди видов можно ввести иерархию, подобную типов теории, а именно, требовать, чтобы элементы вида были определены независимо от определения самого вида. Разумеется, при широком введении видов в интуиционистскую математику в ней возникают проблемы, характерные для абстрактной теории множеств, такие, как предикативность, возникновение антиномий и т. п. Следует, однако, иметь в виду, что, с одной стороны, обращение с видами во многом отлично от обращения с множествами в классич. математике и, с другой стороны, в практически разрабатываемой интуиционистской математике виды занимают весьма скромное место. В действительности подавляющую часть результатов можно сформулировать и доказать вообще без употребления видов как самостоятельных объектов исследования. Это связано с естественной тенденцией И. рассматривать в качестве объекта исследования эффективно конструируемые или эффективно порождаемые объекты. В рамках И. рассматриваются и другие, "нетрадиционные" объекты. Перспективным оказалось изучение эффективных функционалов конечного типа, с помощью к-рых в рамках И. удалось построить интерпретацию для классич. анализа [П. С. Новиков, К. Гёдель (К. Godel), К. Спектор (С. Spector)]. Отказ от рассмотрения актуально заданных бесконечных множеств и требование эффективности всех осуществляемых построений приводят к тому, что нек-рые разделы традиционной математики приобретают в И. весьма необычный вид. Числовой континуум трактуется не как совокупность отдельных точек, а как "среда становления", поток измельчающихся рациональных интервалов. Каждое отдельное интуиционистское действительное число определяется с. с. п., значениями к-рой являются неограниченно уменьшающиеся вложенные друг в друга рациональные интервалы. В рассуждениях об интуиционистском числовом континууме применяются такие специфич. принципы, как бар-индукция и теорема о веере. Следствием этого является, напр., то обстоятельство, что в естественной системе понятий всякая интуиционистская действительная функция, определенная на отрезке, равномерно непрерывна. Интуиционистская математика является достаточно разработанным направлением в математике, содержащим много продвинутых результатов, в том числе и в таких областях, как теория меры, функциональный анализ, топология, теория дифференциальных уравнений. Несколько в стороне от этих исследований стоит попытка Г. Вейля (Н. Weyl, 1918) построить математику на основе предикативного подхода. Соглашаясь в целом с интуиционистской критикой, Г. Вейль предложил ограничиться конструктивными объектами исследования и задавать множества в виде условий в нек-ром языке, определяемом таким образом, чтобы не нарушалась предикативность определения множеств. Впоследствии Г. Вейль присоединился к развитой интуиционистской концепции построения математики, его взгляды положили начало глубоким исследованиям в основаниях математики. Считая критерием верности построений прежде всего интуицию и в противовес формализму, Л. Э. Я. Брауэр возражал против попыток формализации интуиционистской математики и, в частности, интуиционистской логики. Однако значительные успехи в изучении интуиционистской логики были достигнуты именно после того, как ее основные законы были точно сформулированы в виде исчислений, к к-рым можно было применять точные методы мат'ематич. логики. В разработке интуиционистской логики приняли значительное участие и математики, не считающие себя "интуиционистами". Более того, вопрос "веры в интуиционизм" становится второстепенным - специальные интуиционистские исчисления имеют большой чисто математич. интерес, как проясняющие различные идеи эффективности в математике. Современная тенденция в развитии И. сближает его с конструктивной математикой в самом широком понимании последнего термина. После точной формулировки А. Рейтингом (А. Неуting) интуиционистского исчисления предикатов (см. Интуиционистская логика )была открыта топологич. интерпретация этого исчисления [А. Тарский (A. Tarski)] и интерпретация интуиционистского исчисления предикатов в виде исчисления задач (А. Н. Колмогоров). Была доказана независимость логич. связок и невозможность представления интуиционистской логики высказываний в виде конечнозначной логики (К. Гёдель). А. Рейтинг описал интуиционистское арифметическое исчисление, к-рое получается, если классическое арифметич. исчисление рассматривать на базе интуиционистского исчисления предикатов. Для исчисления предикатов и арифметич. исчисления А. Н. Колмогоров и К. Гёдель предложили погружающую операцию классич. исчисления в негативный фрагмент соответствующего интуиционистского исчисления, из к-рой, в частности, следует непротиворечивость классич. исчисления, если интуиционистское считать содержательно истинным. Были установлены свойства интуиционистской дизъюнкции и существования, состоящие в том, что если выводимо утверждение Исследовался вопрос о семантической полноте интуиционистского исчисления предикатов. Исчерпывающая алгебраич. характеристика выводимости дана в теории моделей интуиционистской логики Э. Бета (Е. Beth) и С. Крипке (S. Kripke). Эти теории имеют значительные приложения и в других разделах интуиционистской математики. Интуиционистская логика полна относительно нек-рых концепций с. с. п. и, в то же время, не полна относительно рекурсивной реализуемости. Интуиционистское понимание кванторов позволяет сформулировать в арифметике в виде математич. утверждения Чёрча тезис, напр, в форме: "если для всякого натурального числа хсуществует натуральное y, удовлетворяющее отношению ( х, у), то существует общерекурсивная функция f такая, что для всякого химеет, место ( х,f(x))", при этом отношение ( х, у )не должно содержать неконструктивных параметров типа с. с. п. В языке арифметики можно естественно сформулировать и конструктивного подбора принцип А. А. Маркова. Анализ взаимоотношений этих фундаментальных принципов в интуиционистских теориях является предметом ряда современных исследований. Удовлетворительное построение теории с. с. п. и более высоких разделов интуиционистской математики было завершено к 70-м гг. 20 в. Обычный язык формальной теории интуиционистского анализа содержит два сорта переменных: переменные х, у,z, ... для натуральных чисел и переменные a, b, у,... для с. с. п., перерабатывающих натуральные числа в натуральные. В качестве термов теория содержит символы примитивно-рекурсивных операций над функциями и числами. Атомарные формулы имеют вид равенства двух термов, кванторы употребляются по обоим сортам переменных. Теория содержит все постулаты интуиционистского арифметич. исчисления. Эта группа постулатов обеспечивает возможность вывести в теории все основные свойства примитивно-рекурсивных преобразований чисел и функций. Так, в теории можно описать взаимно однозначный способ кодирования конечных последовательностей ( кортежей )натуральных чисел натуральными числами. Пусть ( х х, ..., х п )означает номер кортежа с числами х 1, ..., х п в качестве членов; х*у есть операция сочленения кортежей, заданных номерами, т. е. если
результаты применения непрерывного оператора к с. с. п. определяются следующим образом: у=a(b)означает
и g=(a|b) означает
Пусть, далее, (b) х означает такую функцию а, что
С помощью приведенных определений можно точно сформулировать несколько фундаментальных принципов, относящихся собственно к с. с. п. Это прежде всего интуиционистская аксиома выбора: принцип непрерывности Брауэра
и бар-индукция. Эти принципы задают формальную теорию с. с. п., предложенную С. Клини, теорию, достаточную для получения в ней всех основных теорем интуиционистского анализа, включая теорему о веере, равномерную непрерывность действительных функций и др. Следует иметь в виду, что эта теория отражает лишь один вид интуиционистских последовательностей, вид, особенно пригодный для построения интуиционистского анализа. Другой характерный вид с. с. п.- беззаконные последовательности, упомянутые выше. Следующий принцип Кранзеля отражает то обстоятельство, что вся информация о беззаконной с. с. п. может быть извлечена лишь путем исследования ее начальных отрезков:
где a - единственный параметр А(a) по с. с. п. Еще один вид с. с. п. возникает при попытке отобразить в формальной теории существование с. с. п., зависящих от решения проблем. Для таких с. с. п. истинна так наз. схема Крипке:
Различные интуиционистские принципы имеют место по отношению к определенным видам с. с. п. Так, для беззаконных последовательностей не выполняется в общем виде интуиционистская аксиома выбора, а последовательности, зависящие от решения проблем, не удовлетворяют принципу непрерывности Брауэра в том его виде, к-рый был указан выше. Гораздо менее разработаны формальные теории для отражения интуиционистской теории видов. Однако и здесь имеются попытки сформулировать специфически интуиционистские способы обращения с видами. Напр., если X- переменная для видов натуральных чисел, то можно принять следующую схему аксиом, предложенную А. Троэльстра [4]:
До 2-й половины 20 в. идеи Л. Э. Я. Брауэра в полном объеме оставались достоянием узкой группы математиков-интуиционистов, хотя они и оказали большое влияние на все дальнейшие исследования по основаниям математики. В последнее время положение изменилось. Развитие теории доказательств позволило оформить в виде точных исчислений основные интуиционистские теории и подвергнуть их точному исследованию. Развитие вычислительной тенденции в математике пробудило интерес к логич. анализу эффективных средств доказательства и изучению абстракций, применяемых в математике. Возникли различные программы конструктивной перестройки математики в той или иной концепции конструктивности. Синтез традиционных методов И. с современными методами теории доказательств позволил значительно продвинуться в И. Лит.:[1] Гейтинг А., Интуиционизм, пер. с англ., М., 1965; [2] Кlееne S. С, Vеslеу R. E., The foundations of intuitionistic mathematics, Amst., 1965; [3] Кrеisel G., Trоelstra A. S., "Ann. Math. Logic", 1970, v. 1, №3, p. 229-387; [4] TroelstraA. S., Metamathematical investigation of intuitionistic Arithmetic and Analysis, В., 1973 (Lect. Notes in Math., №344); [5] Мартин-Лёф П., Очерки по конструктивной математике, пер. с англ., М., 1975; [6] Френкель А., Бар-Хиллел И., Основания теории множеств, пер. с англ., М., 1966. А. Г. Драгалин. |
|
|
|

 суждений Аи Всчитается доказанной, только если исследователь располагает методом доказательства одного из суждений Аили В. С этой точки зрения суждение вида
суждений Аи Всчитается доказанной, только если исследователь располагает методом доказательства одного из суждений Аили В. С этой точки зрения суждение вида 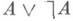 может быть и не истинным, если проблема Ане решена и не опровергнута к настоящему времени. Отсюда видно, что исключенного третьего закон неприемлем в интуиционистской математике в качестве логич. принципа. Истинное математич. суждение представляет собой сообщение о выполненных построениях, и эффективный характер этих построений предполагает использование особой интуиционистской логики, отличной от классической. При этом эффективность в И. понимается достаточно широко, она не обязательно связана с наличием алгоритма в точном понимании этого термина и может носить, напр., характер историч. наступления события, зависеть от фактич. решения проблем, от физич. факторов.
может быть и не истинным, если проблема Ане решена и не опровергнута к настоящему времени. Отсюда видно, что исключенного третьего закон неприемлем в интуиционистской математике в качестве логич. принципа. Истинное математич. суждение представляет собой сообщение о выполненных построениях, и эффективный характер этих построений предполагает использование особой интуиционистской логики, отличной от классической. При этом эффективность в И. понимается достаточно широко, она не обязательно связана с наличием алгоритма в точном понимании этого термина и может носить, напр., характер историч. наступления события, зависеть от фактич. решения проблем, от физич. факторов. то для нек-рого терма tвыводимо A(t), а из выводимости АЪВследует выводимость Аили выводимость В. Некоторый вариант интуиционистского понимания суждений был предложен С. К. Клини (S. С. Kleene) в форме рекурсивной реализуемости. Именно такое понимание характерно для конструктивного направления в математике, развиваемого в Советском Союзе научной школой А. А. Маркова. Понимая термин "И." достаточно широко, можно рассматривать конструктивное направление в математике как разновидность И., для к-рого характерно исследование конструктивных объектов и конструктивных процессов алгоритмич. методами.
то для нек-рого терма tвыводимо A(t), а из выводимости АЪВследует выводимость Аили выводимость В. Некоторый вариант интуиционистского понимания суждений был предложен С. К. Клини (S. С. Kleene) в форме рекурсивной реализуемости. Именно такое понимание характерно для конструктивного направления в математике, развиваемого в Советском Союзе научной школой А. А. Маркова. Понимая термин "И." достаточно широко, можно рассматривать конструктивное направление в математике как разновидность И., для к-рого характерно исследование конструктивных объектов и конструктивных процессов алгоритмич. методами. и
и  то
то 
 Номер одночленного кортежа
Номер одночленного кортежа  обозначим через
обозначим через  Пусть
Пусть  означает кортеж (a(0), . . ., a(n-1)). Введем предикат "а есть непрерывный оператор" следующим определением:
означает кортеж (a(0), . . ., a(n-1)). Введем предикат "а есть непрерывный оператор" следующим определением:  означает
означает







