|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕОПРЕДЕЛЕННОСТЕЙ РАСКРЫТИЕЗначение НЕОПРЕДЕЛЕННОСТЕЙ РАСКРЫТИЕ в математической энциклопедии: - методы вычисления пределов функций, заданных формулами, к-рые в результате формальной подстановки в них предельных значений аргумента теряют смысл, т. е. переходят в выражения типа
по к-рым нельзя судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют. Основным инструментом для раскрытия неопределенностей служит Тейлора формула, с помощью к-рой выделяется главная часть функции. Так, в случае неопределенности типа 0/0, для того чтобы найти предел
где
функции fи g представляют по формуле Тейлора в окрестности точки х 0 (если это возможно) до первого не равного нулю члена:
в результате получается, что
В случае неопределенности типа
где
применяют преобразование
сводящее задачу к раскрытию неопределенности типа 0/0. Неопределенности типа
соответственно. Для раскрытия неопределенностей типа Другим общим методом раскрытия неопределенностей типа Л. Д. Кудрявцев. |
|
|
|

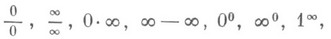
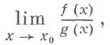
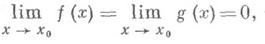
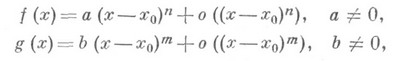
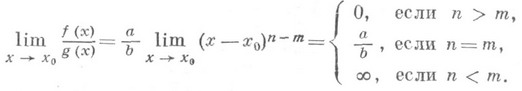
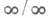 для нахождения предела
для нахождения предела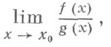
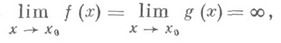
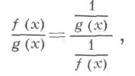
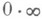 и
и  также целесообразно приводить к виду 0/0 следующими преобразованиями:
также целесообразно приводить к виду 0/0 следующими преобразованиями: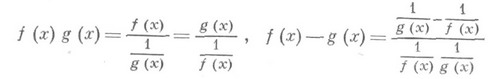
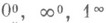 целесообразно первоначально прологарифмировать выражения, предел к-рых требуется найти.
целесообразно первоначально прологарифмировать выражения, предел к-рых требуется найти.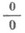 . и .
. и .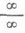 . и сводимых к ним является Лопита ля правило.
. и сводимых к ним является Лопита ля правило.