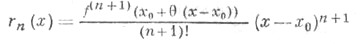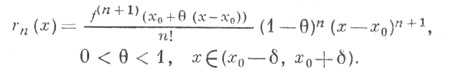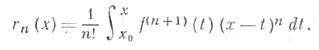|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТЕЙЛОРА ФОРМУЛАЗначение ТЕЙЛОРА ФОРМУЛА в математической энциклопедии: - представление функции в виде суммы еи многочлена Тейлора степени п(n=0, 1, 2, . . .) и остаточного члена. Если действительная функция / одного переменного имеет ппроизводных в точке х 0, то ее Т. ф. имеет вид f(x) = Pn(x) + rn(x),
Если функция f дифференцируема n+1 раз в нек-рой окрестности
где р=1,2, . . ., n+1, частным видом к-рой являются форма Лагpанжа
и форма Коши
Если производная порядка n+1 функции f интегрируема на отрезке с концами в точках хи х 0, то остаточный член можно записать в интегральной форме
Т. ф. со всеми указанными формами записи ее остаточного члена обобщается на случай функций нескольких переменных. Т. ф. справедлива и для отображений подмножеств нормированных пространств в подобные же пространства, причем в этом случае остаточный член может быть записан в форме Пеано и интегральной форме. Лит.:[1] Ильин В. А., Садовничий В. А., Сендов Б. X., Математический анализ, М., 1979: [2] Никольский С. М., Курс математического анализа, 3 изд., т. 1, М., 1983. |
|
|
|

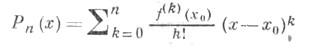
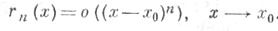
 точки х 0, то остаточный член в этой окрестности может быть записан в форме Шлёмильха - Роша
точки х 0, то остаточный член в этой окрестности может быть записан в форме Шлёмильха - Роша