|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НАИБОЛЬШЕГО ГАРАНТИРОВАННОГО РЕЗУЛЬТАТА ПРИНЦИПЗначение НАИБОЛЬШЕГО ГАРАНТИРОВАННОГО РЕЗУЛЬТАТА ПРИНЦИП в математической энциклопедии: - один из основных принципов принятия решения, используемый в исследовании операций и игр теории. Н. г. р. п. реализуется в стремлении выбрать такую стратегию, чтобы минимальный выигрыш, получаемый в результате ее применения, был максимальным (см. Максимин). В ряде случаев Н. г. р. п. может быть получен как следствие в нек-рой системе аксиом, отдельные аксиомы к-рой указывают на те естественные свойства, к-рыми должен обладать всякий "разумный" принцип оптимального поведения (см. [5]). Конкретизация Н. г. р. п. в различных ситуациях приводит к постановке целого ряда задач на максимин. Исследование операций, т. е. совокупности действий, ведущих к достижению поставленной цели, проводится исследователем операции в интересах оперирующей стороны, к-рая стремится к достижению цели, математически выражаемой желанием увеличить критерий эффективности'- функцию Исходя из информированности исследователя о значениях у, неконтролируемые факторы уподразделяются на три группы: фиксированные факторы, значения к-рых известны; случайные факторы, т. е. случайные процессы с известными законами распределения; неопределенные факторы, для к-рьгх известна только область У, к-рой они принадлежат, или область, к-рой принадлежат их законы распределения. Оценка эффективности стратегий и выбор из них осуществляются исследователем операций на основе получения максимально гарантированной величины критерия эффективности при предполагающейся информированности оперирующей стороны о неконтролируемых факторах. Если
Наибольший гарантированный результат (н. г. р.) определяется как величина
стратегия
является оптимальной в рассматриваемой операции. В случае, когда оперирующая сторона не ожидает информации о конкретных значениях
(см. Минимакса принцип). Если значение уизвестно точно, то для (*) выполняется равенство
Если значения уформируются активным противником, исследователь операции и оперирующая сторона информированы о критерии эффективности противника Конкретизация Н. г. р. п. в играх с фиксированной последовательностью ходов игроков и в операциях, когда информация о неопределенных факторах уточняется во времени, приводит к решению весьма сложных минимаксных задач (напр., дифференциальных игр). Пусть в операции, наряду с неопределенным фактором Если же от повторения к повторению уменяется произвольным образом, то н. г. р. имеет вид
В других случаях (а также в других классах стратегий, напр, вида Смешанной стратегией наз. вероятностная мера
то н. г. р. равен
Большое значение имеет задача вычисления оптимальн. смешанных стратегий (см. Антагонистическая игра). В многошаговых операциях с конечным числом пшагов критерий эффективности имеет вид
где
К подобным минимаксным задачам приводят и нек-рые проблемы теории дифференциальных игр. Для нечетко формулируемой цели оперирующей стороны, когда, напр., имеется набор критериев эффективности
где Последовательное применение Н. г. р. п. в разных условиях информированности оперирующей стороны позволяет единым образом оценить эффективность стратегий и построить полную теорию принятия решения в условиях неопределенности. Лит.:[1] Гермейер Ю. В., Введение в теорию исследования операций, М., 1971; [2] Воробьев Н. Н., "Успехи матем. наук", 1970, т. 25, в. 2, с. 81-140; [3] Гермейер Ю. Б., Игры с непротивоположными интересами, М., 1976; [4] Вентцель Е. С, Исследование операций, М., 1972; [5] Вилка с Э., "Теория вероятн. и ее примен.", 1963, т. 8, № 3, с. 324- 327. Ф. И. Ерешко, В. В. Федоров. |
|
|
|

 где
где  - выбор оперирующей стороны,
- выбор оперирующей стороны, - неконтролируемый оперирующей стороной фактор. Выбор конкретных значений
- неконтролируемый оперирующей стороной фактор. Выбор конкретных значений 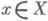 в зависимости от информированности оперирующей стороны и исследователя операции о значениях уопределяет стратегию
в зависимости от информированности оперирующей стороны и исследователя операции о значениях уопределяет стратегию  оперирующей стороны.
оперирующей стороны.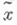 - стратегия оперирующей стороны, то ее оценкой, когда известно лишь, что
- стратегия оперирующей стороны, то ее оценкой, когда известно лишь, что  наз. величина
наз. величина

 , для к-рой
, для к-рой

 , н. г. р. определяется величиной
, н. г. р. определяется величиной


 и при этом увыбирается противником из условия
и при этом увыбирается противником из условия  то н. г. р. определяется величиной
то н. г. р. определяется величиной  где
где 
 есть случайный фактор
есть случайный фактор  с известным законом распределения Р, и оперирующая сторона производит осреднение по случайностям. В этом случае критерием эффективности является математич. ожидание
с известным законом распределения Р, и оперирующая сторона производит осреднение по случайностям. В этом случае критерием эффективности является математич. ожидание  что означает для оперирующей стороны согласие с определенным риском. Как правило, введение
что означает для оперирующей стороны согласие с определенным риском. Как правило, введение  применяется в многократно повторяющихся операциях. Если упри повторениях не меняет своего значения и
применяется в многократно повторяющихся операциях. Если упри повторениях не меняет своего значения и  то н. г. р. равен
то н. г. р. равен 

 н. г. р. выражается иными комбинациями операций взятия экстремума и интегрирования (см. [1], [3]).
н. г. р. выражается иными комбинациями операций взятия экстремума и интегрирования (см. [1], [3]). на
на  . Если, как выше, оперирующая сторона согласна на осреднение критерия эффективности
. Если, как выше, оперирующая сторона согласна на осреднение критерия эффективности


 - выбор оперирующей стороны, а
- выбор оперирующей стороны, а  - значение неконтролируемого фактора на i-м шаге. Н. г. р. в многошаговых операциях записывается, как правило, в виде кратного (последовательного) макси-мина. Так, в антагонистич. игре с полной информацией н. г. р. равен
- значение неконтролируемого фактора на i-м шаге. Н. г. р. в многошаговых операциях записывается, как правило, в виде кратного (последовательного) макси-мина. Так, в антагонистич. игре с полной информацией н. г. р. равен
 и неопределенным фактором для исследователя операций является номер i, данный принцип приводит к свертке критериев, и н. г. р. равен
и неопределенным фактором для исследователя операций является номер i, данный принцип приводит к свертке критериев, и н. г. р. равен
 - уровень, к-рый желательно обеспечить по i-й компоненте. Если величина н. г. р. неотрицательна, желательные уровни достижимы.
- уровень, к-рый желательно обеспечить по i-й компоненте. Если величина н. г. р. неотрицательна, желательные уровни достижимы.