МАКСИМИН

Значение МАКСИМИН в математической энциклопедии:

численные методы- раздел вычислительной математики, посвященный решению максиминных (минимаксных) задач. Задачи вычисления максиминов и минимаксов часто возникают в исследовании операций и теории игр, напр. при использовании минимакса принципа или наибольшего гарантированного результата принципа.

Исходной является задача вычисления М.:

возникающая, напр., при решении антагонистич. игр с полной информацией. Ее естественным обобщением является задача нахождения М. со "связанными" переменными:

причем множество В(х).часто задается в виде

для всякого Эта задача оказывается основной в теории игр двух лиц с обменом информацией (см., напр., Игра с иерархической структурой). Итерирование исходной задачи приводит к задаче кратного, или последовательного, М.:

к-рая связана с решением нек-рых динамич. игр. Представляют интерес стохастич. задачи вычисления М., а также минимаксные задачи оптимального управления. В основе большинства способов решения минимаксных задач лежит градиентный метод или штрафных функций метод. При применении первого из них задачу (1) рассматривают как задачу оптимального программирования

где

Построение численных методов решения задачи (4) - (5) связано с дифференцируемостью по направлению функции минимума (5).

Если - компакт в - производная по направлению (см [1] - [3]),

то в случае конечного множества Yформула (6) позволяет построить итеративную последовательность x₁, х₂, ..., в к-рой для k=0,1, ... и к-рая при нек-рых дополнительных предположениях сходится к точке, удовлетворяющей необходимому условию М.

При использовании метода штрафных функций задача (1) для непрерывной на произведении компакта

и единичного куба функции F(x, у).сводится к нахождению

где

(u - вспомогательная переменная). При этом если пара (u(с), х(с)).реализует максимум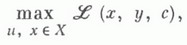

то любая предельная точка (u*, х*).последовательности дает величину

М.(1) и одну из оптимальных стратегий х*, для к-рой

(см. [4]). Тем самым решение задачи (1) с любой точностью сводится к отысканию максимума функции (7) при достаточно больших значениях штрафа с. Избежать трудностей, связанных с вычислением интегралов в (7), позволяет метод стохастич. градиента (см. [5], [8]):

где - стохастич. градиент функции т. е. случайная величина, математич. ожидание к-рой совпадает с

При нек-рых условиях, налагаемых на последовательности {a_k} и {c_k}и функцию F( х, у), для любого начального приближения ( х ₁, у ₁).последовательность, определяемая процессом (8), с вероятностью 1 сходится к множеству решений задачи нахождения М. (1).

Избежать больших значений параметра штрафа св (7) позволяет т. н. "метод невязок" (см. [61), представляющий собой еще один способ преобразования задачи (1). При этом величина и* М. (1) определяется как максимальное значение и, для к-рого

где

Здесь значение х*, реализующее

дает оптимальную стратегию в задаче (1). Отыскивать наибольший корень и* уравнения (9) можно, используя градиентные методы минимизации функции Ф по х.

Методы преобразования задач, основанные на методе штрафных функций, позволяют приближение сводить к задачам на максимум минимаксные задачи со связанными переменными (2) (см. [7], [8]).

Экстремальные задачи, к-рые получаются при сведении минимаксных задач к задачам на максимум, весьма сложны, и их решение известными методами сопряжено с большими, подчас непреодолимыми для современных ЭВМ трудностями. В особенности это относится к проблеме отыскания последовательных М. из (3) при большой кратности.

Наряду с указанными общими подходами к решению минимаксных задач имеется ряд приемов, ориентированных на те или иные частные классы задач, напр. на задачи теории игр двух лиц с передачей информации (см. [6]).

Лит.:[1] Демьянов В. Ф., Малоземов В. Н., Введение в минимакс, М., 1972; [2] Д а н с к и н Д ж. М., Теория максимина, пер. с англ., М., 1970; [3] Д е м ь я н о в В. Ф., Минимакс: дифференцируемость по направлениям, Л., 1974; [4] Г е р м е и е р Ю. Б., Введение в теорию исследования операций, М., 1971; [5] Е р м о л ь е в Ю. М., Методы стохастического программирования, М., 1976; [6] Гермейер Ю. Б., Игры с непротивоположными интересами, М., 1976; [7] Е р е ш к о Ф. И., 3 л о б и н А. С., "Экономика и матем. методы", 1977, т.13, № 4, с. 703-13; [8] Ф е д о р о в В. В., Численные методы максимина, М., 1979. В. В. Федоров.