МНОГОГРАННИК

Значение МНОГОГРАННИК в математической энциклопедии:

- совокупность конечного числа плоских многоугольников такая, что: 1) каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного), называемого смежным с первым (по этой стороне); 2) от любого из многоугольников, составляющих М., можно дойти до любого из них, переходя к смежному с ним, а от этого, в свою очередь, к смежному с ним, и т. д. Эти многоугольники наз. гранями, их стороны - ребрами, а их вершины - вершинами М.

Приведенное определение М. получает различный смысл в зависимости от того, как определить многоугольник. Если под многоугольником понимают плоские замкнутые ломаные (хотя бы и самопересекающиеся), то приходят к первому определению М. Основная часть статьи построена на основе второго определения М., при к-ром его грани являются многоугольниками, понимаемыми как части плоскости, ограниченные ломаными. С этой точки зрения М. есть поверхность, составленная из многоугольных кусков. Если эта поверхность сама себя не пересекает, то она есть полная поверхность нек-рого геометрич. тела, к-рое также наз. М.; отсюда возникает третья точка зрения на М. как на геометрич. тела, причем допускается также существование у этих тел "дырок", ограниченных конечным числом плоских граней.

Простейшими примерами М. являются призмы и пирамиды. М. наз. n-угольной пирамидой, если он имеет одной своей гранью (основанием) какой-либо n-угольник, а остальные грани - треугольники с общей вершиной, не лежащей в плоскости основания. Треугольная пирамида наз. также тетраэдром. М. наз. n-угольной призмой, если он имеет двумя своими гранями (основаниями) равные n-уголь-ники (не лежащие в одной плоскости), получающиеся друг из друга параллельным переносом, а остальные грани - параллелограммы, противоположными сторонами к-рых являются соответственные стороны оснований. Для всякого М. нулевого рода эйлерова характеристика (число вершин минус число ребер плюс число граней) равна двум; символически: В- Р+Г=2 (теорема Эйлера). Для М. рода рсправедливо соотношение В-Р+Г=2-2р.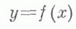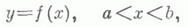

Выпуклым многогранником наз. выпуклая оболочка конечного числа точек, т. е. такой М., к-рый лежит по одну сторону от плоскости любой его грани. Внутренняя его часть есть выпуклое тело. Если поверхность выпуклого тела многогранная, то соответствующий М.- выпуклый. Наиболее важны следующие выпуклые М.

Правильные многогранники (тела Платона) - такие выпуклые М., все грани к-рых суть одинаковые правильные многоугольники и все многогранные углы при вершинах правильные и равные (см. рис. 1- 5).

Изогоны и изоэдры- выпуклые М., все многогранные углы к-рых равны (изогоны) или равны все грани (изоэдры); причем группа поворотов (с отражениями) изогона (изоэдра) вокруг центра тяжести переводит любую его вершину (грань) в любую другую его вершину (грань). Каждый из изоэдров может быть реализован так, что все его грани суть правильные многоугольники. Полученные так М. наз. полуправильными многогранниками (телами Архимеда) (см. рис. 10-25).

Параллелоэдра (выпуклые) - М., рассматриваемые пак тела, параллельным пересечением к-рых можно заполнить все бесконечное пространство так, чтобы они не входили друг в друга и не оставляли пустот между собой, т. е. образовали разбиение пространства (см. рис. 26-30).

Основываясь на первом (указанном в начале статьи) определении М., можно указать еще четыре правильных невыпуклых М. (тела Пуансо). В этих М. либо грани пересекают друг друга, либо сами грани - самопересекающиеся многоугольники (см. рис. 6-9). Для изучения вопросов, связанных с площадями поверхностей и объемами таких М., удобно пользоваться именно первым определением М.

Если у М. можно так ориентировать грани, чтобы каждое ребро в тех двух гранях, к-рые смежны по этому ребру, имело бы обратные направления, то его наз. ориентируемым, в противном случае - неориентируемым. Для ориентируемого М. (даже если он - самопересекающийся и его грани - самопересекающиеся многоугольники) можно ввести понятия площади поверхности и величины объема. Площадью ориентируемого М. наз. сумму площадей его граней. При определении объема следует иметь в виду, что совокупность внутренних кусков граней М. разделяет пространство на определенное число связных кусков, из к-рых один по отношению к М. бесконечный (внешний), а остальные конечные (внутренние). Если из внешней по отношению к М. точки провести отрезок в какую-либо внутреннюю точку внутреннего куска, то сумму "коэффициентов" тех внутренних кусков граней М., к-рые пересечет этот отрезок, наз. коэффициентом рассматриваемого внутреннего куска М. (она не зависит от выбора внешней точки); такой коэффициент есть целое положительное, отрицательное число или нуль. Сумму обычных объемов всех внутренних кусков М., умноженных на эти их коэффициенты, наз. объемом М.

Рассматриваются п n-мерные М. Некоторые из указанных определений имеют n-мерное обобщение. В частности, найдены все выпуклые правильные M., при n=4 их оказалось 6, а при всех больших n всего 3: обобщение тетраэдра, куба и октаэдра. В то же время, напр., неизвестны (1982) все 4-мерные изоэдры и изогоны.

Лит.:[1] Энциклопедия элементарной математики, кн. 4 - Геометрия, М., 1963; [2] Гильберт Д., Кон-Фоссен С, Наглядная геометрия, пер. с нем., 3 изд., М.- Л., 1981; [3] Александров А. Д., Выпуклые многогранники, М.- Л., 1950; [4] Люстерник Л. А., Выпуклые фигуры и многогранники, М., 1956; [5] Bruckner M., Vielecke und Vielflache. Theorie und Geschichte, Lpz., 1900.

По материалам одноименной статьи из БСЭ-3.