|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛОКАЛЬНЫЕ ГОМОЛОГИИЗначение ЛОКАЛЬНЫЕ ГОМОЛОГИИ в математической энциклопедии: гомологии группы  определенные в точках  по открытым окрестностям Uточки х, а для гомологически локально связных X - также с обратными пределами  Гомологическая размерность конечномерного метризуемого локально компактного пространства Xнад Gсовпадает с наибольшим значением n, для к-рого Пусть С *. - дифференциальный пучок над X, определяемый сопоставлением каждому открытому множеству Лит.:[1] Скляренко Е. Г., "Изв. АН СССР. Сер. матем.", 1971, т. 35, № 4, с. 831-43; [2] Xарлап А. Э., "Матем. сб.", 1975, т. 96, .№ 3, с. 347-73. Е. Г. Скляренко. |
|
|
|

 -
-  причем множество таких точек
причем множество таких точек  имеет размерность п.
имеет размерность п. комплекса цепей
комплекса цепей  Группы
Группы  являются слоями производных пучков
являются слоями производных пучков 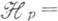
 Для обобщенных многообразий
Для обобщенных многообразий  при
при  = dim X. В этом случае гомологич. последовательность с коэффициентами в G пары (X, А )совпадает с когомологнями пары (X, ХА).с коэффициентами в пучке
= dim X. В этом случае гомологич. последовательность с коэффициентами в G пары (X, А )совпадает с когомологнями пары (X, ХА).с коэффициентами в пучке  (двойственность Пуанкаре - Л е ф ш е ц а). Для локальных когомологии локально компактных пространств аналогичные факты не имеют места.
(двойственность Пуанкаре - Л е ф ш е ц а). Для локальных когомологии локально компактных пространств аналогичные факты не имеют места.