"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГОМОЛОГИИ С КОМПАКТНЫМИ НОСИТЕЛЯМИ
Значение ГОМОЛОГИИ С КОМПАКТНЫМИ НОСИТЕЛЯМИ в математической энциклопедии:
теория частично точных гомологии (см. Гомологии теория), удовлетворяющая следующей аксиоме о компактных носителях: для каждого элемента hиз r-мерной группы  произвольной пары пространств
произвольной пары пространств  в теории Нсуществует такая компактная пара
в теории Нсуществует такая компактная пара  , что hсодержится в образе индуцированного вложением гомоморфизма
, что hсодержится в образе индуцированного вложением гомоморфизма

Если теория Нточна и имеет компактные носители, то справедлива следующая теорема: для любого элемента 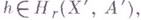 принадлежащего ядру гомоморфизма ц, существует такая компактная пара
принадлежащего ядру гомоморфизма ц, существует такая компактная пара  , что
, что

и hпринадлежит ядру гомоморфизма

Точная теория обладает компактными носителями тогда и только тогда, когда для любой пары  группа
группа  есть прямой предел
есть прямой предел  где
где  пробегает компактные пары, содержащиеся в
пробегает компактные пары, содержащиеся в  . Точная теория гомологии с компактными носителями единственна на категории произвольных (некомпактных) полиэдральных пар при данной группе коэффициентов и она эквивалентна сингулярной теории. Наряду с группой
. Точная теория гомологии с компактными носителями единственна на категории произвольных (некомпактных) полиэдральных пар при данной группе коэффициентов и она эквивалентна сингулярной теории. Наряду с группой  имеется группа
имеется группа

где  - компактные подпары из
- компактные подпары из 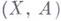 . Сингулярная группа гомологии обладает компактными носителями и изоморфна группе
. Сингулярная группа гомологии обладает компактными носителями и изоморфна группе  . В спектральной теории, кроме групп
. В спектральной теории, кроме групп 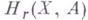 гомологии Александрова - Чеха и групп
гомологии Александрова - Чеха и групп  рассматривается также группа, являющаяся образом при естественном гомоморфизме
рассматривается также группа, являющаяся образом при естественном гомоморфизме 
эта группа, как и группа  удовлетворяет аксиоме о компактных носителях, но в спектральной теории группой Г. с к. н. обычно называют именно группу
удовлетворяет аксиоме о компактных носителях, но в спектральной теории группой Г. с к. н. обычно называют именно группу  Х Указанные три группы спектральной теории отличны друг от друга и каждая из них является объектом теоремы двойственности как при дискретной, так и при компактной группе коэффициентов (см. Двойственность в топологии).
Х Указанные три группы спектральной теории отличны друг от друга и каждая из них является объектом теоремы двойственности как при дискретной, так и при компактной группе коэффициентов (см. Двойственность в топологии).
Лит.:[1] Стинрод Н., Эйленберг С., Основания алгебраической топологии, пер. с англ., М., 1958; 12] Александров П. С., "Матем. сб.", 1947, т. 21, вып. 2, c. 161-232; [3] Спеньер Э., Алгебраическая топология, пер Сангл., М., 1971. Г. С. Чогошвили.

 произвольной пары пространств
произвольной пары пространств  в теории Нсуществует такая компактная пара
в теории Нсуществует такая компактная пара  , что hсодержится в образе индуцированного вложением гомоморфизма
, что hсодержится в образе индуцированного вложением гомоморфизма 
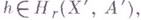 принадлежащего ядру гомоморфизма ц, существует такая компактная пара
принадлежащего ядру гомоморфизма ц, существует такая компактная пара  , что
, что 

 группа
группа  есть прямой предел
есть прямой предел  где
где  пробегает компактные пары, содержащиеся в
пробегает компактные пары, содержащиеся в  . Точная теория гомологии с компактными носителями единственна на категории произвольных (некомпактных) полиэдральных пар при данной группе коэффициентов и она эквивалентна сингулярной теории. Наряду с группой
. Точная теория гомологии с компактными носителями единственна на категории произвольных (некомпактных) полиэдральных пар при данной группе коэффициентов и она эквивалентна сингулярной теории. Наряду с группой  имеется группа
имеется группа 
 - компактные подпары из
- компактные подпары из 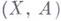 . Сингулярная группа гомологии обладает компактными носителями и изоморфна группе
. Сингулярная группа гомологии обладает компактными носителями и изоморфна группе  . В спектральной теории, кроме групп
. В спектральной теории, кроме групп 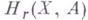 гомологии Александрова - Чеха и групп
гомологии Александрова - Чеха и групп  рассматривается также группа, являющаяся образом при естественном гомоморфизме
рассматривается также группа, являющаяся образом при естественном гомоморфизме 
 удовлетворяет аксиоме о компактных носителях, но в спектральной теории группой Г. с к. н. обычно называют именно группу
удовлетворяет аксиоме о компактных носителях, но в спектральной теории группой Г. с к. н. обычно называют именно группу  Х Указанные три группы спектральной теории отличны друг от друга и каждая из них является объектом теоремы двойственности как при дискретной, так и при компактной группе коэффициентов (см. Двойственность в топологии).
Х Указанные три группы спектральной теории отличны друг от друга и каждая из них является объектом теоремы двойственности как при дискретной, так и при компактной группе коэффициентов (см. Двойственность в топологии).