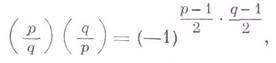" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ГАУССА ЗАКОН ВЗАИМНОСТИ

Значение ГАУССА ЗАКОН ВЗАИМНОСТИ в математической энциклопедии:

соотношение, связывающее значения Лежандра символов для различных нечетных простых чисел р и q(см. Квадратичный закон взаимности). Кроме основного Г. з. в. для квадратичных вычетов, заключающегося в соотношении:

имеются еще два дополнения к указанному закону, а именно:

Закон взаимности для квадратичных вычетов был впервые высказан Л. Эйлером (L. Euler, 1772). А. Ле-жандр (A. Legendre, 1785) дал формулировку закона в современной форме и доказал часть этого закона. Первое полное доказательство Г. з. в. было дано К. Гауссом (С. Gauss, 1801) (см. [1]). В течение жизни К. Гаусс дал восемь различных доказательств квадратичного закона взаимности, построенных на различных принципах.

Попытки установить закон взаимности для кубических и биквадратичных вычетов привели К. Гаусса к введению кольца целых комплексных чисел.

Лит.: [1] Гаусс К. Ф., Труды по теории чисел, пер. с нем. и латин., М., 1959; [2] Виноградов И. М., Основы теории чисел, 8 изд., М., 1972; [3] Xассе Г., Лекции по теории чисел, пер. с нем., М., 1953. С. А. Степанов.