"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГАРМОНИЧЕСКОЕ ПРОСТРАНСТВО
Значение ГАРМОНИЧЕСКОЕ ПРОСТРАНСТВО в математической энциклопедии:
топология, пространство X с пучком 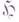 непрерывных действительных функций с аксиоматически фиксируемыми в той или иной форме тремя основными свойствами классических гармонических функций:свойство сходимости, выражаемое второй Гарнака теоремой;принцип экстремума; разрешимость Дирихле задачи для достаточно широкого класса открытых множеств из X. Функции пучка
непрерывных действительных функций с аксиоматически фиксируемыми в той или иной форме тремя основными свойствами классических гармонических функций:свойство сходимости, выражаемое второй Гарнака теоремой;принцип экстремума; разрешимость Дирихле задачи для достаточно широкого класса открытых множеств из X. Функции пучка 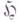 получают наименование гармонич. функций; преимущество этого аксиоматич. подхода состоит в том, что с его помощью в теорию включаются решения не только Лапласа уравнения, но и нек-рых других уравнений эллиптич. и параболич. типов. Пусть X - локально компактное топологич. пространство. Под пучком функций на Xздесь понимается отображение
получают наименование гармонич. функций; преимущество этого аксиоматич. подхода состоит в том, что с его помощью в теорию включаются решения не только Лапласа уравнения, но и нек-рых других уравнений эллиптич. и параболич. типов. Пусть X - локально компактное топологич. пространство. Под пучком функций на Xздесь понимается отображение  определенное на семействе всех открытых множеств
определенное на семействе всех открытых множеств 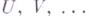 из
из 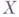 и такое, что: 1)
и такое, что: 1) 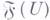 есть семейство функций на U; 2) если
есть семейство функций на U; 2) если  то сужение любой функции из
то сужение любой функции из 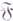 (V).на Uпринадлежит
(V).на Uпринадлежит 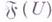 ; 3) для любого семейства
; 3) для любого семейства 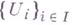 функция на
функция на 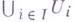 принадлежит
принадлежит  если для всех
если для всех 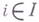 ее сужение на
ее сужение на  принадлежит
принадлежит  Пучок функций
Пучок функций  наз. гипергармоническим, если
наз. гипергармоническим, если 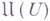 для любого
для любого 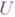 есть выпуклый конус полунепрерывных и конечных снизу действительных функций на
есть выпуклый конус полунепрерывных и конечных снизу действительных функций на  . Пучок функций
. Пучок функций 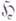 наз. гармоническим, если
наз. гармоническим, если 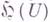 для любого
для любого 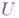 есть действительное векторное пространство непрерывных функций на U;в дальнейшем используется только гармонич. пучок
есть действительное векторное пространство непрерывных функций на U;в дальнейшем используется только гармонич. пучок
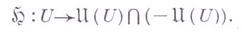
Локально компактное пространство Xназ. Т. <п., если выполняются следующие аксиомы (см. [3]).
Аксиома положительности: пучок 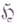 невырожден во всех точках
невырожден во всех точках  , т. е. для любого
, т. е. для любого  существует функция
существует функция  , определенная в окрестности д-, причем
, определенная в окрестности д-, причем 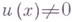 .
.
Аксиома сходимости: если возрастающая последовательность функций из  локально ограничена, то она сходится к функции из
локально ограничена, то она сходится к функции из 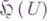 .
.
Аксиома разрешимости: существует базис разрешимых открытых множеств U, т. е. таких, что для любой непрерывной функции f с компактным носителем на 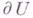 существует обобщенное в смысле Винера - Перрона (см. Перрона метод).решение задачи Дирихле для Uиз
существует обобщенное в смысле Винера - Перрона (см. Перрона метод).решение задачи Дирихле для Uиз 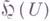 .
.
Аксиома мажоранты: если полунепрерывная и конечная снизу функция 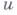 на
на 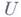 для любого относительно компактного множества
для любого относительно компактного множества 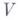 такого, что
такого, что  удовлетворяет условию
удовлетворяет условию
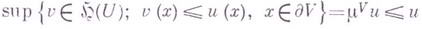
на V, то 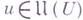 .
.
Евклидово пространство 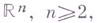 с пучком клас-снч. решений уравнения Лапласа или теплопроводности уравнения образует Г. п. Имеется ряд других вариантов аксиоматики гармонич. пространств. Г. п. локально связны, не содержат изолированных точек; они имеют базис из связных разрешимых множеств.
с пучком клас-снч. решений уравнения Лапласа или теплопроводности уравнения образует Г. п. Имеется ряд других вариантов аксиоматики гармонич. пространств. Г. п. локально связны, не содержат изолированных точек; они имеют базис из связных разрешимых множеств.
Гипергармонич. функция ина Г. п. Xназ. супергармонической, если для любого относительно компактного разрешимого множества Vнаибольшая миноранта 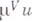 есть гармонич. функция. Положительная супергармонич. функция, для к-рой любая гармонич. миноранта тождественно равна нулю, наз. потенциалом. Г. п. Xназ.
есть гармонич. функция. Положительная супергармонич. функция, для к-рой любая гармонич. миноранта тождественно равна нулю, наз. потенциалом. Г. п. Xназ. 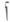 -гармоническим (или
-гармоническим (или 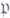 -гармоническим), если для любого
-гармоническим), если для любого 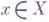 существует положительная супергармонич. функция и(пли, соответственно, потенциал и).на Xтакая, что
существует положительная супергармонич. функция и(пли, соответственно, потенциал и).на Xтакая, что 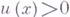
Любое Г. п. допускает покрытие такими открытыми множествами U, для к-рых выполняется принцип минимума в следующей форме: если гипергармоническая функция  положительна вне пересечения Uс любым компактом из Xи
положительна вне пересечения Uс любым компактом из Xи
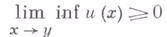
для всех 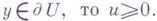 В случае
В случае  -гармонич. пространства этот принцип минимума выполняется для всех открытых множеств. Евклидово пространство
-гармонич. пространства этот принцип минимума выполняется для всех открытых множеств. Евклидово пространство 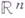 с пучком классич. решений уравнения Лапласа при
с пучком классич. решений уравнения Лапласа при  образует
образует 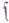 -гармонич. пространство, а при
-гармонич. пространство, а при  оно образует
оно образует 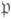 -гармонич. пространство; пространство
-гармонич. пространство; пространство 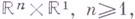 с пучком решений уравнения теплопроводности образует p-гармонич. пространство.
с пучком решений уравнения теплопроводности образует p-гармонич. пространство.
Основными вопросами теории Г. п. являются: теория разрешимости задачи Дирихле, включающая исследование поведения обобщенного решения этой задачи в граничных точках; теория емкости множеств в Г. п.; изучение проблемы выметания (см. Выметания метод).и Робе на задачи.
Лит.:[1] Вrе1оt M., Lectures on potential theory, Bombay, 1960; [2] Bauer H., Harmonische Raume imd ihre Potentialtheorie, В., 1966 (Lecture Notes in Mathematics, № 22); [3] Constantinescu C., Cornea A., Potential theory on harmonic spaces, В., 1972: [4] Брело М., О топологиях и границах в теории потенциала, пер. с англ., М., 1974.
Е. Д. Соломенцев.

 непрерывных действительных функций с аксиоматически фиксируемыми в той или иной форме тремя основными свойствами классических гармонических функций:свойство сходимости, выражаемое второй Гарнака теоремой;принцип экстремума; разрешимость Дирихле задачи для достаточно широкого класса открытых множеств из X. Функции пучка
непрерывных действительных функций с аксиоматически фиксируемыми в той или иной форме тремя основными свойствами классических гармонических функций:свойство сходимости, выражаемое второй Гарнака теоремой;принцип экстремума; разрешимость Дирихле задачи для достаточно широкого класса открытых множеств из X. Функции пучка 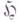 получают наименование гармонич. функций; преимущество этого аксиоматич. подхода состоит в том, что с его помощью в теорию включаются решения не только Лапласа уравнения, но и нек-рых других уравнений эллиптич. и параболич. типов. Пусть X - локально компактное топологич. пространство. Под пучком функций на Xздесь понимается отображение
получают наименование гармонич. функций; преимущество этого аксиоматич. подхода состоит в том, что с его помощью в теорию включаются решения не только Лапласа уравнения, но и нек-рых других уравнений эллиптич. и параболич. типов. Пусть X - локально компактное топологич. пространство. Под пучком функций на Xздесь понимается отображение  определенное на семействе всех открытых множеств
определенное на семействе всех открытых множеств 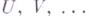 из
из 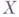 и такое, что: 1)
и такое, что: 1) 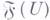 есть семейство функций на U; 2) если
есть семейство функций на U; 2) если  то сужение любой функции из
то сужение любой функции из 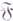 (V).на Uпринадлежит
(V).на Uпринадлежит 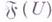 ; 3) для любого семейства
; 3) для любого семейства 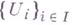 функция на
функция на 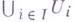 принадлежит
принадлежит  если для всех
если для всех 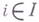 ее сужение на
ее сужение на  принадлежит
принадлежит  Пучок функций
Пучок функций  наз. гипергармоническим, если
наз. гипергармоническим, если 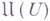 для любого
для любого 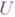 есть выпуклый конус полунепрерывных и конечных снизу действительных функций на
есть выпуклый конус полунепрерывных и конечных снизу действительных функций на  . Пучок функций
. Пучок функций 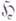 наз. гармоническим, если
наз. гармоническим, если 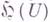 для любого
для любого 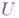 есть действительное векторное пространство непрерывных функций на U;в дальнейшем используется только гармонич. пучок
есть действительное векторное пространство непрерывных функций на U;в дальнейшем используется только гармонич. пучок 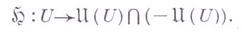
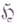 невырожден во всех точках
невырожден во всех точках  , т. е. для любого
, т. е. для любого  существует функция
существует функция  , определенная в окрестности д-, причем
, определенная в окрестности д-, причем 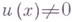 .
. локально ограничена, то она сходится к функции из
локально ограничена, то она сходится к функции из 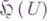 .
.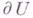 существует обобщенное в смысле Винера - Перрона (см. Перрона метод).решение задачи Дирихле для Uиз
существует обобщенное в смысле Винера - Перрона (см. Перрона метод).решение задачи Дирихле для Uиз 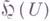 .
.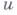 на
на 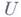 для любого относительно компактного множества
для любого относительно компактного множества 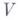 такого, что
такого, что  удовлетворяет условию
удовлетворяет условию 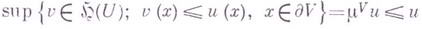
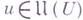 .
.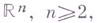 с пучком клас-снч. решений уравнения Лапласа или теплопроводности уравнения образует Г. п. Имеется ряд других вариантов аксиоматики гармонич. пространств. Г. п. локально связны, не содержат изолированных точек; они имеют базис из связных разрешимых множеств.
с пучком клас-снч. решений уравнения Лапласа или теплопроводности уравнения образует Г. п. Имеется ряд других вариантов аксиоматики гармонич. пространств. Г. п. локально связны, не содержат изолированных точек; они имеют базис из связных разрешимых множеств.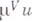 есть гармонич. функция. Положительная супергармонич. функция, для к-рой любая гармонич. миноранта тождественно равна нулю, наз. потенциалом. Г. п. Xназ.
есть гармонич. функция. Положительная супергармонич. функция, для к-рой любая гармонич. миноранта тождественно равна нулю, наз. потенциалом. Г. п. Xназ. 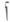 -гармоническим (или
-гармоническим (или 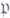 -гармоническим), если для любого
-гармоническим), если для любого 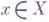 существует положительная супергармонич. функция и(пли, соответственно, потенциал и).на Xтакая, что
существует положительная супергармонич. функция и(пли, соответственно, потенциал и).на Xтакая, что 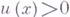
 положительна вне пересечения Uс любым компактом из Xи
положительна вне пересечения Uс любым компактом из Xи 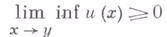
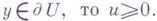 В случае
В случае  -гармонич. пространства этот принцип минимума выполняется для всех открытых множеств. Евклидово пространство
-гармонич. пространства этот принцип минимума выполняется для всех открытых множеств. Евклидово пространство 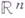 с пучком классич. решений уравнения Лапласа при
с пучком классич. решений уравнения Лапласа при  образует
образует 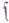 -гармонич. пространство, а при
-гармонич. пространство, а при  оно образует
оно образует 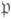 -гармонич. пространство; пространство
-гармонич. пространство; пространство 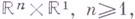 с пучком решений уравнения теплопроводности образует p-гармонич. пространство.
с пучком решений уравнения теплопроводности образует p-гармонич. пространство.