"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ
Значение ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ в математической энциклопедии:
синусоидальное колебание,- периодическое изменение во времени физич. величины, записываемое аналитически в виде

где  - значение колеблющейся величины в момент времени
- значение колеблющейся величины в момент времени  - амплитуда,
- амплитуда,  - циклическая (круговая) частота,
- циклическая (круговая) частота,  - начальная фаза колебаний. Продолжительность одного полного колебания, равная
- начальная фаза колебаний. Продолжительность одного полного колебания, равная  наз. периодом Г. к., а величина
наз. периодом Г. к., а величина  , равная числу полных колебаний в единицу времени, наз. частотой Г. к. (
, равная числу полных колебаний в единицу времени, наз. частотой Г. к. ( ). Период Г. к. не зависит от амплитуды. Скорость, ускорение и все высшие производные гармонически колеблющейся величины изменяются гармонически с той же частотой. На фазовой плоскости
). Период Г. к. не зависит от амплитуды. Скорость, ускорение и все высшие производные гармонически колеблющейся величины изменяются гармонически с той же частотой. На фазовой плоскости Г. к. изображается эллипсом. В природе из-за диссипации энергии абсолютно точные Г. к. не встречаются. Однако существует много важных процессов, близких к Г. к. Таковы малые колебания механич. систем относительно их устойчивого положения равновесия. Получающиеся при этом частоты (так наз. собственные частоты) колебаний не зависят от начальных условий движения, а определяются лишь самой колеблющейся системой как таковой. Напр., малые колебания (под действием силы тяжести) математич. маятника на нити длины lописываются дифференциальным уравнением
Г. к. изображается эллипсом. В природе из-за диссипации энергии абсолютно точные Г. к. не встречаются. Однако существует много важных процессов, близких к Г. к. Таковы малые колебания механич. систем относительно их устойчивого положения равновесия. Получающиеся при этом частоты (так наз. собственные частоты) колебаний не зависят от начальных условий движения, а определяются лишь самой колеблющейся системой как таковой. Напр., малые колебания (под действием силы тяжести) математич. маятника на нити длины lописываются дифференциальным уравнением

где  - ускорение силы тяжести, а
- ускорение силы тяжести, а  - угол между вертикалью и нитью маятника. Общее решение этого уравнения имеет вид
- угол между вертикалью и нитью маятника. Общее решение этого уравнения имеет вид  где (собственная) частота колебаний
где (собственная) частота колебаний  зависит только от gи l, а амплитуда Аи фаза
зависит только от gи l, а амплитуда Аи фаза  являются постоянными интегрирования, выбираемыми на основе начальных условий.
являются постоянными интегрирования, выбираемыми на основе начальных условий.
Г. к. играют большую роль в изучении общих колебаний, так как сложные периодически и почти периодически меняющиеся величины могут быть с любой степенью точности представлены суммой различных Г. к. Математически это соответствует приближению функций тригонометрич. рядами и Фурье интегралами.
Классический ряд Фурье

комплекснозначной функции  , определенной на
, определенной на  может рассматриваться как разложение
может рассматриваться как разложение  на сумму Г. к. с целочисленными частотами
на сумму Г. к. с целочисленными частотами 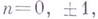
 Коэффициент Фурье
Коэффициент Фурье

определяет амплитуду  и сдвиг фазы
и сдвиг фазы 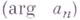 Г. к. частоты п. Совокупность всех коэффициентов Фурье определяет спектр
Г. к. частоты п. Совокупность всех коэффициентов Фурье определяет спектр  и показывает, какие Г. к. действительно входят в
и показывает, какие Г. к. действительно входят в  и каковы амплитуды и начальные фазы этих колебаний. Знание спектра заменяет знание функции
и каковы амплитуды и начальные фазы этих колебаний. Знание спектра заменяет знание функции  .
.
Функцию  определенную на
определенную на  уже нельзя построить из Г. к. с целочисленными частотами. Для ее построения нужны колебания всех частот: функция
уже нельзя построить из Г. к. с целочисленными частотами. Для ее построения нужны колебания всех частот: функция  представляется в виде интеграла Фурье
представляется в виде интеграла Фурье
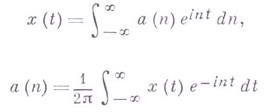
- спектральная плотность функции  .
.
Эти представления функций являются основой Фурье методов решения различных задач в теории дифференциальных и интегральных уравнений.
Лит.:[1] Горелик Г. С., Колебания и волны, 2 изд., М., 1959. Л. П. Купцов.


 - значение колеблющейся величины в момент времени
- значение колеблющейся величины в момент времени  - амплитуда,
- амплитуда,  - циклическая (круговая) частота,
- циклическая (круговая) частота,  - начальная фаза колебаний. Продолжительность одного полного колебания, равная
- начальная фаза колебаний. Продолжительность одного полного колебания, равная  наз. периодом Г. к., а величина
наз. периодом Г. к., а величина  , равная числу полных колебаний в единицу времени, наз. частотой Г. к. (
, равная числу полных колебаний в единицу времени, наз. частотой Г. к. ( ). Период Г. к. не зависит от амплитуды. Скорость, ускорение и все высшие производные гармонически колеблющейся величины изменяются гармонически с той же частотой. На фазовой плоскости
). Период Г. к. не зависит от амплитуды. Скорость, ускорение и все высшие производные гармонически колеблющейся величины изменяются гармонически с той же частотой. На фазовой плоскости Г. к. изображается эллипсом. В природе из-за диссипации энергии абсолютно точные Г. к. не встречаются. Однако существует много важных процессов, близких к Г. к. Таковы малые колебания механич. систем относительно их устойчивого положения равновесия. Получающиеся при этом частоты (так наз. собственные частоты) колебаний не зависят от начальных условий движения, а определяются лишь самой колеблющейся системой как таковой. Напр., малые колебания (под действием силы тяжести) математич. маятника на нити длины lописываются дифференциальным уравнением
Г. к. изображается эллипсом. В природе из-за диссипации энергии абсолютно точные Г. к. не встречаются. Однако существует много важных процессов, близких к Г. к. Таковы малые колебания механич. систем относительно их устойчивого положения равновесия. Получающиеся при этом частоты (так наз. собственные частоты) колебаний не зависят от начальных условий движения, а определяются лишь самой колеблющейся системой как таковой. Напр., малые колебания (под действием силы тяжести) математич. маятника на нити длины lописываются дифференциальным уравнением 
 - ускорение силы тяжести, а
- ускорение силы тяжести, а  - угол между вертикалью и нитью маятника. Общее решение этого уравнения имеет вид
- угол между вертикалью и нитью маятника. Общее решение этого уравнения имеет вид  где (собственная) частота колебаний
где (собственная) частота колебаний  зависит только от gи l, а амплитуда Аи фаза
зависит только от gи l, а амплитуда Аи фаза  являются постоянными интегрирования, выбираемыми на основе начальных условий.
являются постоянными интегрирования, выбираемыми на основе начальных условий.
 , определенной на
, определенной на  может рассматриваться как разложение
может рассматриваться как разложение  на сумму Г. к. с целочисленными частотами
на сумму Г. к. с целочисленными частотами 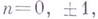
 Коэффициент Фурье
Коэффициент Фурье 
 и сдвиг фазы
и сдвиг фазы 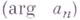 Г. к. частоты п. Совокупность всех коэффициентов Фурье определяет спектр
Г. к. частоты п. Совокупность всех коэффициентов Фурье определяет спектр  и показывает, какие Г. к. действительно входят в
и показывает, какие Г. к. действительно входят в  и каковы амплитуды и начальные фазы этих колебаний. Знание спектра заменяет знание функции
и каковы амплитуды и начальные фазы этих колебаний. Знание спектра заменяет знание функции  .
. определенную на
определенную на  уже нельзя построить из Г. к. с целочисленными частотами. Для ее построения нужны колебания всех частот: функция
уже нельзя построить из Г. к. с целочисленными частотами. Для ее построения нужны колебания всех частот: функция  представляется в виде интеграла Фурье
представляется в виде интеграла Фурье 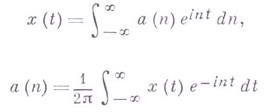
 .
.