|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГАРМОНИЧЕСКИЙ МНОГОЧЛЕНЗначение ГАРМОНИЧЕСКИЙ МНОГОЧЛЕН в математической энциклопедии: - 1) Г. м.- многочлен по переменным где : - число размещений из ппо тс тповторениями. Однородные Г. м. где Лит.:[1] Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; [2] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966; [3] Брело М., Основы классической теории потенциала, пер. с франц., М., 1964. Е. Д. Соломенцев. 2) Г. м.- конечная линейная комбинация гармоник. Действительнозначные Г. м. представимы в виде при нек-ром натуральном N, неотрицательных Ак, действительных при натуральных значениях |
|
|
|

 удовлетворяющий Лапласа уравнению. Любой Г. м. может быть представлен в виде суммы однородных Г. м. При
удовлетворяющий Лапласа уравнению. Любой Г. м. может быть представлен в виде суммы однородных Г. м. При  среди однородных Г. м. степени тимеется только два линейно независимых, напр, действительная и мнимая части в выражении
среди однородных Г. м. степени тимеется только два линейно независимых, напр, действительная и мнимая части в выражении  При
При  число линейно независимых однородных Г. м. степени
число линейно независимых однородных Г. м. степени  равно
равно  В общем случае
В общем случае  число линейно независимых однородных Г. м. степени
число линейно независимых однородных Г. м. степени  равно
равно 

 наз. также шаровыми функциями (в особенности при
наз. также шаровыми функциями (в особенности при  ). При
). При  введение сферич. координат позволяет записать:
введение сферич. координат позволяет записать:
 есть сферическая функция степени т.
есть сферическая функция степени т.
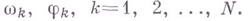 Комплекс-позначные Г. м. представимы в виде
Комплекс-позначные Г. м. представимы в виде 
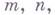 действительных значениях
действительных значениях  и комплексных значениях
и комплексных значениях 
 Г. м. являются простейшими почти периодическими функциями В. Ф. Емельянов.
Г. м. являются простейшими почти периодическими функциями В. Ф. Емельянов.