|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГАРМОНИЧЕСКАЯ МЕРАЗначение ГАРМОНИЧЕСКАЯ МЕРА в математической энциклопедии: понятие теории гармонических функций, возникшее в связи с проблемами оценки модуля аналитич. функции внутри области, когда известны те или иные оценки модуля на границе области (см. [1], [2]). Пусть D - ограниченное открытое множество евклидова пространства полученная Ш.-Ж. Валле Пуссеном [3] выметания методом. Более того, если Е- произвольное борелевское множество на Г, то Г. м. Основные свойства Г. м: если D - область и В последнем случае Еназ. множеством нулевой Г. м. Если компактное множество С точки зрения приложений к теории функций комплексного переменного особенно важное значение имеет зависимость Г. м. от области D, выражаемая гармонической меры, принципом, сущность к-рого состоит в том, что при отображениях области D, осуществляемых однозначными аналитич. функциями Явное вычисление Г. м. удается провести лишь для простейших областей D(прежде всего, для круга и шара, полуплоскости, полупространства; см. Пуассона интеграл). Поэтому важное значение имеют различные методы оценки (см. [4]-[7]) Г. м., базирующиеся в основном на расширения области принципе. В простейшей форме при n=2 он состоит в следующем: пусть конечносвязная область Dограничена конечным числом жордановых кривых Лит.:[1] Carleman Т., "Ark. mat.", J921, Bd 15, № 10, p. 1-7; [2] Nevanlinna F., Nevanlinna R., "Acta Soc. scent, fennica", 1922, n. 50, № 5; [3] de la Vallee Poussin Ch.-J., "Ann. Inst. H. Poincarg", 1932, v. 2, p. 169-232; [4] Неванлинна Р., Однозначные аналитические функции, пер. с нем., М.- Л., 1941; [5] Голувин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [6] Брело М., Основы классической теории потенциала, пер. с франц., М., 1964; [7] Наlistе К., "Ark. mat.", 1965, Bd 6, № 1, p. 1-31. Е. Д. Соломенцев. |
|
|
|


 - граница
- граница  - конечная действительная непрерывная функция на Г. Каждой такой функции f соответствует единственная гармония, функция
- конечная действительная непрерывная функция на Г. Каждой такой функции f соответствует единственная гармония, функция  на D, являющаяся для f обобщенным решением Дирихле задачи. Если считать точку
на D, являющаяся для f обобщенным решением Дирихле задачи. Если считать точку  фиксированной, то функционал Н f(x).определяет на компактном множестве Г положительную борелевскую меру
фиксированной, то функционал Н f(x).определяет на компактном множестве Г положительную борелевскую меру 
 к-рая и называется гармонической мерой в точке х. Для всякой непрерывной на Г функции f справедлива формула представления обобщенного решения задачи Дирихле
к-рая и называется гармонической мерой в точке х. Для всякой непрерывной на Г функции f справедлива формула представления обобщенного решения задачи Дирихле 
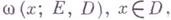 Множества Ев точке хравна значению в хобобщенного решения задачи Дирихле для характеристпч. функции
Множества Ев точке хравна значению в хобобщенного решения задачи Дирихле для характеристпч. функции  ,
,  , множества Е.
, множества Е. - гармонич. функция точки хна D;
- гармонич. функция точки хна D;
 хвтя бы в одной точке хО D, то
хвтя бы в одной точке хО D, то 
 имеет нулевую Г. м. относительно какой-либо одной области D,
имеет нулевую Г. м. относительно какой-либо одной области D,  , то есть
, то есть  то оно имеет нулевую Г. м. относительно любой другой области
то оно имеет нулевую Г. м. относительно любой другой области  то есть Кесть множество нулевой абсолютной Г. м. Множество Кимеет нулевую абсолютную Г. <м. тогда и только тогда, когда оно имеет нулевую (гармоническую) емкость.
то есть Кесть множество нулевой абсолютной Г. м. Множество Кимеет нулевую абсолютную Г. <м. тогда и только тогда, когда оно имеет нулевую (гармоническую) емкость. , хО D, Г. м. не убывает. В частности, при взаимно однозначном конформном отображении Г. м. не изменяется.
, хО D, Г. м. не убывает. В частности, при взаимно однозначном конформном отображении Г. м. не изменяется. - дуги, лежащие, на Г. Тогда, если область Dрасширяется каким-либо образом через дополнительную часть
- дуги, лежащие, на Г. Тогда, если область Dрасширяется каким-либо образом через дополнительную часть  границы, то Г. м.
границы, то Г. м.  может только увеличиться.
может только увеличиться.