"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГАРМОНИЧЕСКАЯ МАЖОРАНТА
Значение ГАРМОНИЧЕСКАЯ МАЖОРАНТА в математической энциклопедии:
наименьшая гармоническая мажоранта  семейства
семейства  - нижняя огибающая семейства
- нижняя огибающая семейства  всех супергармонич. мажорант vk , семейства
всех супергармонич. мажорант vk , семейства  субгармонич. функций на открытом множестве Dевклидова пространства
субгармонич. функций на открытом множестве Dевклидова пространства  т. е.
т. е.

Г. м.  либо является гармонич. функцией, либо
либо является гармонич. функцией, либо  В случае семейства, состоящего из одной функции и, субгармонической на более широком множестве
В случае семейства, состоящего из одной функции и, субгармонической на более широком множестве  иногда используется также понятие наилучшей Г. м.
иногда используется также понятие наилучшей Г. м.  - решения обобщенной задачи Дирихле для Dпо значениям ина границе
- решения обобщенной задачи Дирихле для Dпо значениям ина границе  Всегда
Всегда  причем справедлива формула [1]
причем справедлива формула [1]

где  - ассоциированная с имера,
- ассоциированная с имера,  - (обобщенная) функция Грина задачи Дирихле для D. Наилучшая н наименьшая Г. м. совпадают тогда и только тогда, когда множество всех иррегулярных точек Г имеет
- (обобщенная) функция Грина задачи Дирихле для D. Наилучшая н наименьшая Г. м. совпадают тогда и только тогда, когда множество всех иррегулярных точек Г имеет  -меру нуль.
-меру нуль.
Соответственно, если 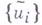 - семейство супергармонич. функций на D, то наибольшая гармоническая миноранта
- семейство супергармонич. функций на D, то наибольшая гармоническая миноранта  семейства
семейства  определяется как верхняя огибающая семейства всех субгармонич. минорант семейства
определяется как верхняя огибающая семейства всех субгармонич. минорант семейства  ; при этом
; при этом  есть наименьшая Г. м. для семейства
есть наименьшая Г. м. для семейства  .
.
Другую постановку вопроса о Г. м., связанную с задачей Коши для уравнения Лапласа, см. в ст. Гармоническая функция.
Лит.:[l] Frostman О., Potentiel d'equilibre et capacite des ensembles avec qvielques applications a la theorie des fonctions, Lund, 1935; [2] Брело М., Основы классической теории потенциала, пер. с франц., М., 1964, гл. 2, 9. Е. <Д. Соломенцев.

 семейства
семейства  - нижняя огибающая семейства
- нижняя огибающая семейства  всех супергармонич. мажорант vk , семейства
всех супергармонич. мажорант vk , семейства  субгармонич. функций на открытом множестве Dевклидова пространства
субгармонич. функций на открытом множестве Dевклидова пространства  т. е.
т. е.
 либо является гармонич. функцией, либо
либо является гармонич. функцией, либо  В случае семейства, состоящего из одной функции и, субгармонической на более широком множестве
В случае семейства, состоящего из одной функции и, субгармонической на более широком множестве  иногда используется также понятие наилучшей Г. м.
иногда используется также понятие наилучшей Г. м.  - решения обобщенной задачи Дирихле для Dпо значениям ина границе
- решения обобщенной задачи Дирихле для Dпо значениям ина границе  Всегда
Всегда  причем справедлива формула [1]
причем справедлива формула [1]
 - ассоциированная с имера,
- ассоциированная с имера,  - (обобщенная) функция Грина задачи Дирихле для D. Наилучшая н наименьшая Г. м. совпадают тогда и только тогда, когда множество всех иррегулярных точек Г имеет
- (обобщенная) функция Грина задачи Дирихле для D. Наилучшая н наименьшая Г. м. совпадают тогда и только тогда, когда множество всех иррегулярных точек Г имеет  -меру нуль.
-меру нуль.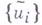 - семейство супергармонич. функций на D, то наибольшая гармоническая миноранта
- семейство супергармонич. функций на D, то наибольшая гармоническая миноранта  семейства
семейства  определяется как верхняя огибающая семейства всех субгармонич. минорант семейства
определяется как верхняя огибающая семейства всех субгармонич. минорант семейства  ; при этом
; при этом  есть наименьшая Г. м. для семейства
есть наименьшая Г. м. для семейства  .
.