"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГАЛУА КОГОМОЛОГИИ
Значение ГАЛУА КОГОМОЛОГИИ в математической энциклопедии:
- когомологии Галуа группы. Если М - абелева группа и  - группа Галуа расширения
- группа Галуа расширения 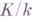 , действующая на М, то когомологии Галуа есть группы когомологии
, действующая на М, то когомологии Галуа есть группы когомологии

определяемые комплексом  состоит из всех отображений
состоит из всех отображений 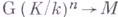 , a d - кограничный оператор (см. Когомологии групп). Если K/k- расширение бесконечной степени, то дополнительно требуется, чтобы Галуа топологическая группа непрерывно действовала на дискретной группе М, а за коцепи
, a d - кограничный оператор (см. Когомологии групп). Если K/k- расширение бесконечной степени, то дополнительно требуется, чтобы Галуа топологическая группа непрерывно действовала на дискретной группе М, а за коцепи  берутся непрерывные отображения.
берутся непрерывные отображения.
Для неабелевой группы Мсодержательно определяются только нульмерные ( Н°).и одномерные ( Н 1) когомологии. А именно, 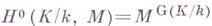 - множество неподвижных точек группы G(K/k).в М, а
- множество неподвижных точек группы G(K/k).в М, а  - фактормножество множества одномерных коциклов, т. е. непрерывных отображений г:
- фактормножество множества одномерных коциклов, т. е. непрерывных отображений г:  удовлетворяющих соотношению
удовлетворяющих соотношению

для всех  по отношению эквивалентности - (где
по отношению эквивалентности - (где  тогда и только тогда, когда
тогда и только тогда, когда 
 для некоторого
для некоторого  и всех
и всех  В неабелевом случае
В неабелевом случае  является множеством с отмеченной точкой, соответствующей тривиальному коциклу
является множеством с отмеченной точкой, соответствующей тривиальному коциклу  (где е - единица М), и структурой группы, вообще говоря, не обладает. Тем не менее и для таких когомологии можно развить стандартный когомологич. формализм (см. Неабелевы когомологии).
(где е - единица М), и структурой группы, вообще говоря, не обладает. Тем не менее и для таких когомологии можно развить стандартный когомологич. формализм (см. Неабелевы когомологии).
Если  - сепарабельное замыкание поля k, то принято группу
- сепарабельное замыкание поля k, то принято группу  обозначать
обозначать  и вместо
и вместо  писать
писать  .
.
Г. к. в форме, несколько отличной от современной, возникли еще в работах Д. Гильберта (D. Hilbert), Э. Артина (Е. Artin), Р. Брауэра (R. Brauer), X. Хассе (Н. Hasse), К. Шевалле (С. Chevalley) по теории полей классов, конечномерным простым алгебрам и квадратичным формам. Развитие идей и методов гомологич. алгебры обусловили введение в начале 50-х гг. 20 в. Г. к. конечных расширений со значениями в абелевой группе в работах Э. Артина, А. Вейля (A. Weil), Г. Хохшильда (G. Hochschild), Дж. Тейта (J. Tate) в связи с потребностями теории полей классов. В общем случае теория абелевых Г. к. была затем развита Дж. Тейтом и Ж. П. Серром (см. [1], [3], [6]).
С помощью Г. к. Дж. Тейтом было введено понятие когомологич. размерности группы Галуа G к, поля k, к-рая обозначается  . Она определяется через когомологическую р-р азмерность
. Она определяется через когомологическую р-р азмерность  - наименьшее целое число птакое, что для всякого периодического G к -модуля Аи всякого целого
- наименьшее целое число птакое, что для всякого периодического G к -модуля Аи всякого целого  р-примарная компонента группы
р-примарная компонента группы  равна нулю. Когомологическая размерность
равна нулю. Когомологическая размерность  есть
есть

Для всякого алгебраически замкнутого поля k  для всех полей таких , что Брауэра группа В (К).их любого конечного расширения K/k тривиальна, cd
для всех полей таких , что Брауэра группа В (К).их любого конечного расширения K/k тривиальна, cd  для р-адического поля, поля алгебраич. функций одной переменной с конечным полем констант и для чисто мнимого числового поля
для р-адического поля, поля алгебраич. функций одной переменной с конечным полем констант и для чисто мнимого числового поля  (см. [1]). Поля k, когомологич. размерность группы Галуа к-рых
(см. [1]). Поля k, когомологич. размерность группы Галуа к-рых  , и группа Брауэра
, и группа Брауэра  наз. полями размерности
наз. полями размерности  н это. обозначается
н это. обозначается 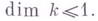 К таким полям относятся все конечные поля, максимальные неразветвленные расширения р-адических полей, поле рациональных функций от одной переменной с алгебраически замкнутым полем констант. Если группа Галуа
К таким полям относятся все конечные поля, максимальные неразветвленные расширения р-адических полей, поле рациональных функций от одной переменной с алгебраически замкнутым полем констант. Если группа Галуа  является про-р-группой, т. е. проективным пределом конечных р-групп, то размерность
является про-р-группой, т. е. проективным пределом конечных р-групп, то размерность  над
над 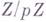 равна минимальному числу топологических образующих группы
равна минимальному числу топологических образующих группы  , а размерность
, а размерность  есть число определяющих соотношений между этими образующими. Если
есть число определяющих соотношений между этими образующими. Если  , то
, то  - свободная про-р-группа.
- свободная про-р-группа.
Неабелевы Г. к. появились в конце 50-х гг. 20 в., однако систематич. исследования начались лишь в 60-х гг. и стимулировались главным образом проблемой классификации алгебраич. групп над алгебраически незамкнутыми полями.
Одной из основных задач, давших толчок развитию неабелевых Г. к., является задача классификации главных однородных пространств групповых схем. Особенно эффективными оказываются Г. к. для проблемы классификации форм алгебраич. многообразий.
Упомянутые выше задачи приводят к проблеме вычисления Г. к. алгебраич. групп. Общие теоремы о строении алгебраич. групп в существенном сводят изучение Г. к. к отдельному рассмотрению Г. к. конечных групп, унипотентных групп, торов, полупростых групп, абелевых многообразий.
Г. к. связной унипотентной группы Uтривиальны, если Uопределена над совершенным полем k, т. е.  для произвольной унипотентной группы U, и
для произвольной унипотентной группы U, и  для всех
для всех  , если U - абелева группа. В частности, для аддитивной группы произвольного поля
, если U - абелева группа. В частности, для аддитивной группы произвольного поля  всегда
всегда  Для несовершенного поля k, вообще говоря,
Для несовершенного поля k, вообще говоря,
Одним из первых существенных фактов о Г. к. была "теорема 90" Гильберта, одна из формулировок к-рой утверждает, что  Кроме того, и для любого k-разложимого алгебраич. тора Твсегда
Кроме того, и для любого k-разложимого алгебраич. тора Твсегда 
 . В общем случае вычисление
. В общем случае вычисление  для произвольного k-определенного тора Тсводится к вычислению
для произвольного k-определенного тора Тсводится к вычислению  где К - минимальное поле разложения Т, что пока (1977) сделано только для специальных полей. Особенно важен для приложений случай, когда k - поле алгебраич. чисел. Для этого случая получены теоремы двойственности, имеющие разнообразные применения.
где К - минимальное поле разложения Т, что пока (1977) сделано только для специальных полей. Особенно важен для приложений случай, когда k - поле алгебраич. чисел. Для этого случая получены теоремы двойственности, имеющие разнообразные применения.
Пусть  - расширение Галуа конечной степени,
- расширение Галуа конечной степени,  - группа аделей мультипликативной K-группы
- группа аделей мультипликативной K-группы  ,
,  - группа характеров тора. Теорема двойственности утверждает, что
- группа характеров тора. Теорема двойственности утверждает, что  -произведение:
-произведение:

задает невырожденное спаривание при  С помощью этой теоремы найдена формула, выражающая Тамагавы числа тора Тчерез инварианты, связанные с его Г. к. Существуют и другие важные теоремы двойственности для Г. к. [1].
С помощью этой теоремы найдена формула, выражающая Тамагавы числа тора Тчерез инварианты, связанные с его Г. к. Существуют и другие важные теоремы двойственности для Г. к. [1].
Доказана [11] тривиальность  над полями kразмерности
над полями kразмерности  . Выделен естественный класс полей, обладающих лишь конечным числом расширений фиксированной степени [так наз. поля типа (F)];к ним относится, напр., поле р-адических чисел. Доказано, что для произвольной алгебраич. группы G над полем kтипа (F).группа когомологий
. Выделен естественный класс полей, обладающих лишь конечным числом расширений фиксированной степени [так наз. поля типа (F)];к ним относится, напр., поле р-адических чисел. Доказано, что для произвольной алгебраич. группы G над полем kтипа (F).группа когомологий  является конечным множеством (см. [1]).
является конечным множеством (см. [1]).
Теория Г. к. полупростых алгебраич. групп имеет глубокие арифметич. и аналитич. рименения. Теорема Кнезера- Брюа- Титса утверждает, что  для односвязных полупростых алгебраич. групп G над локальными полями k, поле вычетов к-рых имеет когомологич. размерность =<1. Эта теорема была доказана сначала для полей р-адических чисел [12], а затем в [7] было получено единообразное доказательство в общем случае. Доказана [13] тривиальность H1(k, G) для поля алгебраич. функций от одной переменной с конечным полем констант. Во всех этих случаях когомологич. размерность
для односвязных полупростых алгебраич. групп G над локальными полями k, поле вычетов к-рых имеет когомологич. размерность =<1. Эта теорема была доказана сначала для полей р-адических чисел [12], а затем в [7] было получено единообразное доказательство в общем случае. Доказана [13] тривиальность H1(k, G) для поля алгебраич. функций от одной переменной с конечным полем констант. Во всех этих случаях когомологич. размерность  и это подтверждает общую гипотезу Ж. П. Серра о тривиальности
и это подтверждает общую гипотезу Ж. П. Серра о тривиальности  для односвязных полупростых G над полями kс
для односвязных полупростых G над полями kс  .
.
Пусть k - глобальное поле, V - множество всех неэквивалентных нормировании  - пополнение k. Вложения
- пополнение k. Вложения  индуцируют естественное отображение
индуцируют естественное отображение

для произвольной k-определенной алгебраич. группы С, ядро к-рого обозначается Ш (G) и в случае абелевых многообразий наз. группой Шафаревича - Тейта. Группа Ш (G).показывает в какой мере Г. к. над глобальным полем определяются Г. к. над локализациями. Для линейных алгебраич. групп основной результат о  принадлежит А. Борелю (A. Borel), к-рый доказал конечность группы
принадлежит А. Борелю (A. Borel), к-рый доказал конечность группы  . Существует гипотеза, что группа
. Существует гипотеза, что группа  конечна и в случае абелевых многообразий. Выделяется случай, когда
конечна и в случае абелевых многообразий. Выделяется случай, когда  т. е. отображение iинъективно. Тогда говорят, что для Gсправедлив Хассе принцип. Такое название объясняется тем, что для ортогональной группы инъективность iэквивалентна классич. теореме Минковского - Хассе о квадратичных формах, а для проективной группы - теореме Брауэра - Хассе - Нётер о расщеплении простых алгебр. Существует также гипотеза, принадлежащая Ж. П. Серру, что для односвязной или присоединенной полупростой группы всегда Ш(G) = 0. Это утверждение доказано для большинства одно-связных полупростых групп над числовыми глобальными полями (исключая группы, имеющие простые компоненты типа E8 ).(см. [13]), а также для любых односвязных алгебраич. групп над функциональными глобальными полями.
т. е. отображение iинъективно. Тогда говорят, что для Gсправедлив Хассе принцип. Такое название объясняется тем, что для ортогональной группы инъективность iэквивалентна классич. теореме Минковского - Хассе о квадратичных формах, а для проективной группы - теореме Брауэра - Хассе - Нётер о расщеплении простых алгебр. Существует также гипотеза, принадлежащая Ж. П. Серру, что для односвязной или присоединенной полупростой группы всегда Ш(G) = 0. Это утверждение доказано для большинства одно-связных полупростых групп над числовыми глобальными полями (исключая группы, имеющие простые компоненты типа E8 ).(см. [13]), а также для любых односвязных алгебраич. групп над функциональными глобальными полями.
Лит.:[1] Серр Ж.-П., Когомологий Галуа, пер. с франц., М., 1968; [2] его же, Алгебраические группы и поля классов, пер. с франц., М., 1968; [31 Алгебраическая теория чисел, пер. с англ., М., 1969; [4] Кох X., Теория Галуа р-расшире-ний, пер. с нем., М., 1973; [5] Art in E., Tate J., Class field theory, N. Y.- Amst., 1967; [6] Sеrrе J.-P., Corps locaux. P., 1962; [7] Воrе1 A., Sеrrе J.-P., "Comra. Math. Helv.", 1964, v. 39, p. Ill-64; [8] Аrtin M., Grоthendieck A., Verdier J.-L., Theorie des topos et cohomologie etale des schemas, t. 1-3, B.- Hdlb. - N. Y., 1972; [9] BruhatF., Tits J.,"Publ. Math. IHES", 1972, № 41, p. 5-252; [10] Borel А., там же, 1963, № 16, p. 5-30; [11] Steinberg R., там же, 1965, № 25, p. 49-80; [12] К n e-zer M., "Math. Z.", 1965, Bd 88, S. 40-47; Bd 89, S. 250-72; [13] Harder G., "Math. Z.", 1965, Bd 90, S. 404-28; 1966, Bd 92, S. 396-415. E. А. Нисневич, В. П. Платонов.

 - группа Галуа расширения
- группа Галуа расширения 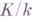 , действующая на М, то когомологии Галуа есть группы когомологии
, действующая на М, то когомологии Галуа есть группы когомологии 
 состоит из всех отображений
состоит из всех отображений 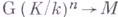 , a d - кограничный оператор (см. Когомологии групп). Если K/k- расширение бесконечной степени, то дополнительно требуется, чтобы Галуа топологическая группа непрерывно действовала на дискретной группе М, а за коцепи
, a d - кограничный оператор (см. Когомологии групп). Если K/k- расширение бесконечной степени, то дополнительно требуется, чтобы Галуа топологическая группа непрерывно действовала на дискретной группе М, а за коцепи  берутся непрерывные отображения.
берутся непрерывные отображения.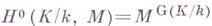 - множество неподвижных точек группы G(K/k).в М, а
- множество неподвижных точек группы G(K/k).в М, а  - фактормножество множества одномерных коциклов, т. е. непрерывных отображений г:
- фактормножество множества одномерных коциклов, т. е. непрерывных отображений г:  удовлетворяющих соотношению
удовлетворяющих соотношению 
 по отношению эквивалентности - (где
по отношению эквивалентности - (где  тогда и только тогда, когда
тогда и только тогда, когда 
 для некоторого
для некоторого  и всех
и всех  В неабелевом случае
В неабелевом случае  является множеством с отмеченной точкой, соответствующей тривиальному коциклу
является множеством с отмеченной точкой, соответствующей тривиальному коциклу  (где е - единица М), и структурой группы, вообще говоря, не обладает. Тем не менее и для таких когомологии можно развить стандартный когомологич. формализм (см. Неабелевы когомологии).
(где е - единица М), и структурой группы, вообще говоря, не обладает. Тем не менее и для таких когомологии можно развить стандартный когомологич. формализм (см. Неабелевы когомологии). - сепарабельное замыкание поля k, то принято группу
- сепарабельное замыкание поля k, то принято группу  обозначать
обозначать  и вместо
и вместо  писать
писать  .
. . Она определяется через когомологическую р-р азмерность
. Она определяется через когомологическую р-р азмерность  - наименьшее целое число птакое, что для всякого периодического G к -модуля Аи всякого целого
- наименьшее целое число птакое, что для всякого периодического G к -модуля Аи всякого целого  р-примарная компонента группы
р-примарная компонента группы  равна нулю. Когомологическая размерность
равна нулю. Когомологическая размерность  есть
есть 
 для всех полей таких , что Брауэра группа В (К).их любого конечного расширения K/k тривиальна, cd
для всех полей таких , что Брауэра группа В (К).их любого конечного расширения K/k тривиальна, cd  для р-адического поля, поля алгебраич. функций одной переменной с конечным полем констант и для чисто мнимого числового поля
для р-адического поля, поля алгебраич. функций одной переменной с конечным полем констант и для чисто мнимого числового поля  (см. [1]). Поля k, когомологич. размерность группы Галуа к-рых
(см. [1]). Поля k, когомологич. размерность группы Галуа к-рых  , и группа Брауэра
, и группа Брауэра  наз. полями размерности
наз. полями размерности  н это. обозначается
н это. обозначается 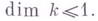 К таким полям относятся все конечные поля, максимальные неразветвленные расширения р-адических полей, поле рациональных функций от одной переменной с алгебраически замкнутым полем констант. Если группа Галуа
К таким полям относятся все конечные поля, максимальные неразветвленные расширения р-адических полей, поле рациональных функций от одной переменной с алгебраически замкнутым полем констант. Если группа Галуа  является про-р-группой, т. е. проективным пределом конечных р-групп, то размерность
является про-р-группой, т. е. проективным пределом конечных р-групп, то размерность  над
над 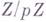 равна минимальному числу топологических образующих группы
равна минимальному числу топологических образующих группы  , а размерность
, а размерность  есть число определяющих соотношений между этими образующими. Если
есть число определяющих соотношений между этими образующими. Если  , то
, то  - свободная про-р-группа.
- свободная про-р-группа. для произвольной унипотентной группы U, и
для произвольной унипотентной группы U, и  для всех
для всех  , если U - абелева группа. В частности, для аддитивной группы произвольного поля
, если U - абелева группа. В частности, для аддитивной группы произвольного поля  всегда
всегда  Для несовершенного поля k, вообще говоря,
Для несовершенного поля k, вообще говоря,
 Кроме того, и для любого k-разложимого алгебраич. тора Твсегда
Кроме того, и для любого k-разложимого алгебраич. тора Твсегда 
 . В общем случае вычисление
. В общем случае вычисление  для произвольного k-определенного тора Тсводится к вычислению
для произвольного k-определенного тора Тсводится к вычислению  где К - минимальное поле разложения Т, что пока (1977) сделано только для специальных полей. Особенно важен для приложений случай, когда k - поле алгебраич. чисел. Для этого случая получены теоремы двойственности, имеющие разнообразные применения.
где К - минимальное поле разложения Т, что пока (1977) сделано только для специальных полей. Особенно важен для приложений случай, когда k - поле алгебраич. чисел. Для этого случая получены теоремы двойственности, имеющие разнообразные применения. - расширение Галуа конечной степени,
- расширение Галуа конечной степени,  - группа аделей мультипликативной K-группы
- группа аделей мультипликативной K-группы  ,
,  - группа характеров тора. Теорема двойственности утверждает, что
- группа характеров тора. Теорема двойственности утверждает, что  -произведение:
-произведение:
 С помощью этой теоремы найдена формула, выражающая Тамагавы числа тора Тчерез инварианты, связанные с его Г. к. Существуют и другие важные теоремы двойственности для Г. к. [1].
С помощью этой теоремы найдена формула, выражающая Тамагавы числа тора Тчерез инварианты, связанные с его Г. к. Существуют и другие важные теоремы двойственности для Г. к. [1]. над полями kразмерности
над полями kразмерности  . Выделен естественный класс полей, обладающих лишь конечным числом расширений фиксированной степени [так наз. поля типа (F)];к ним относится, напр., поле р-адических чисел. Доказано, что для произвольной алгебраич. группы G над полем kтипа (F).группа когомологий
. Выделен естественный класс полей, обладающих лишь конечным числом расширений фиксированной степени [так наз. поля типа (F)];к ним относится, напр., поле р-адических чисел. Доказано, что для произвольной алгебраич. группы G над полем kтипа (F).группа когомологий  является конечным множеством (см. [1]).
является конечным множеством (см. [1]). для односвязных полупростых алгебраич. групп G над локальными полями k, поле вычетов к-рых имеет когомологич. размерность =<1. Эта теорема была доказана сначала для полей р-адических чисел [12], а затем в [7] было получено единообразное доказательство в общем случае. Доказана [13] тривиальность H1(k, G) для поля алгебраич. функций от одной переменной с конечным полем констант. Во всех этих случаях когомологич. размерность
для односвязных полупростых алгебраич. групп G над локальными полями k, поле вычетов к-рых имеет когомологич. размерность =<1. Эта теорема была доказана сначала для полей р-адических чисел [12], а затем в [7] было получено единообразное доказательство в общем случае. Доказана [13] тривиальность H1(k, G) для поля алгебраич. функций от одной переменной с конечным полем констант. Во всех этих случаях когомологич. размерность  и это подтверждает общую гипотезу Ж. П. Серра о тривиальности
и это подтверждает общую гипотезу Ж. П. Серра о тривиальности  для односвязных полупростых G над полями kс
для односвязных полупростых G над полями kс  .
. - пополнение k. Вложения
- пополнение k. Вложения  индуцируют естественное отображение
индуцируют естественное отображение 
 принадлежит А. Борелю (A. Borel), к-рый доказал конечность группы
принадлежит А. Борелю (A. Borel), к-рый доказал конечность группы  . Существует гипотеза, что группа
. Существует гипотеза, что группа  конечна и в случае абелевых многообразий. Выделяется случай, когда
конечна и в случае абелевых многообразий. Выделяется случай, когда  т. е. отображение iинъективно. Тогда говорят, что для Gсправедлив Хассе принцип. Такое название объясняется тем, что для ортогональной группы инъективность iэквивалентна классич. теореме Минковского - Хассе о квадратичных формах, а для проективной группы - теореме Брауэра - Хассе - Нётер о расщеплении простых алгебр. Существует также гипотеза, принадлежащая Ж. П. Серру, что для односвязной или присоединенной полупростой группы всегда Ш(G) = 0. Это утверждение доказано для большинства одно-связных полупростых групп над числовыми глобальными полями (исключая группы, имеющие простые компоненты типа E8 ).(см. [13]), а также для любых односвязных алгебраич. групп над функциональными глобальными полями.
т. е. отображение iинъективно. Тогда говорят, что для Gсправедлив Хассе принцип. Такое название объясняется тем, что для ортогональной группы инъективность iэквивалентна классич. теореме Минковского - Хассе о квадратичных формах, а для проективной группы - теореме Брауэра - Хассе - Нётер о расщеплении простых алгебр. Существует также гипотеза, принадлежащая Ж. П. Серру, что для односвязной или присоединенной полупростой группы всегда Ш(G) = 0. Это утверждение доказано для большинства одно-связных полупростых групп над числовыми глобальными полями (исключая группы, имеющие простые компоненты типа E8 ).(см. [13]), а также для любых односвязных алгебраич. групп над функциональными глобальными полями.