|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГАЛИЛЕЯ ПРЕОБРАЗОВАНИЕЗначение ГАЛИЛЕЯ ПРЕОБРАЗОВАНИЕ в математической энциклопедии: преобразование, определяющее в классич. механике переход от одной инерциальной системы отсчета к другой, движущейся относительно первой прямолинейно и равномерно. При этом система отсчета понимается как четырехмерная, позволяющая фиксировать три пространственные координаты и отсчет часов (время). Если задана инерциальная система отсчета где Основные законы классич. механики инвариантны относительно Г. п., но, напр., уравнение распространения фронта световой волны (электромагнитное явление) не инвариантно относительно Г. п. По этой причине Г. п. были обобщены X. Лоренцом (Н. Lo-rentz, см. Лоренца преобразование). Эти преобразования легли в основу специальной теории относительности. Преобразования Лоренца переходят в Г. п. при Г. п. образуют группу, являющуюся подгруппой группы неоднородных преобразований Галилея, называемой группой Галилея, к-рая получается из группы Г. п. добавлением преобразований смещения начала координат в трехмерном пространстве и начала отсчета времени. А. 3. Петров. |
|
|
|

 , то во всякой другой инерциальной системе
, то во всякой другой инерциальной системе 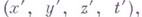 движущейся относительно нее прямолинейно и равномерно, координаты
движущейся относительно нее прямолинейно и равномерно, координаты  связаны (с точностью до переноса начала и поворота осей) с координатами
связаны (с точностью до переноса начала и поворота осей) с координатами  преобразованиями Галилея
преобразованиями Галилея 
 - компоненты скорости движения системы
- компоненты скорости движения системы  относительно системы
относительно системы 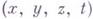 .
. .
.