"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЬЕТОРИСА ГОМОЛОГИИ
Значение ВЬЕТОРИСА ГОМОЛОГИИ в математической энциклопедии:
одна из первых теорий гомологии, определенных в неполиэдральном случае.
Впервые их рассмотрел Л. Брауэр (L. Brouwer, 1911) (в плоском случае), а затем Л. Вьеторис (L. Vietoris, 1927) распространил его определение на произвольные подмножества евклидова (и даже метрического) пространства.
Под (упорядоченным) n-мерным симплексом tn подмножества Аметрич. пространства X понимается упорядоченное подмножество  в Ас условием
в Ас условием  После этого определяются
После этого определяются  -цепи множества Апо данной группе коэффициентов Gкак формальные конечные линейные комбинации
-цепи множества Апо данной группе коэффициентов Gкак формальные конечные линейные комбинации 
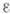 -симплексов
-симплексов  с коэффициентами
с коэффициентами  Граница
Граница 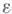 симплекса
симплекса  определяется так:
определяется так: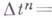
 это -
это -  -цепь. По линейности определяются граница любой
-цепь. По линейности определяются граница любой  -цепи, и
-цепи, и  -циклы как
-циклы как  -цепи с нулевой границей,
-цепи с нулевой границей,  -цепь
-цепь  множества
множества  -гомологична нулю в А (взаписи
-гомологична нулю в А (взаписи  ), если
), если  для нек-рой
для нек-рой  -цепи
-цепи  в А.
в А.
Истинным циклом, множества Аназ. последовательность  в к-рой
в к-рой  есть
есть  -цикл в А, и
-цикл в А, и  . Истинные циклы образуют группу
. Истинные циклы образуют группу  (A, G). Истинный цикл z гомологичен нулю в А, если для любого
(A, G). Истинный цикл z гомологичен нулю в А, если для любого  существует такое N, что все
существует такое N, что все  при
при 
 -гомологичны нулю в А. Обозначим
-гомологичны нулю в А. Обозначим 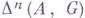 факторгруппу группы
факторгруппу группы 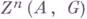 по подгруппе
по подгруппе  циклов, гомологичных нулю.
циклов, гомологичных нулю.
Цикл zназ. сходящимся, если для любого  существует такое N, что любые два цикла
существует такое N, что любые два цикла  при
при  -гомологичны между собою в А. Обозначим группу сходящихся циклов
-гомологичны между собою в А. Обозначим группу сходящихся циклов 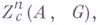 и пусть
и пусть  -соответствующая факторгруппа.
-соответствующая факторгруппа.
Цикл z имеет компактный носитель, если существует такой компакт  , что все вершины всех симплексов всех циклов
, что все вершины всех симплексов всех циклов  лежат в F. Аналогично изменим понятие гомологичности нулю цикла, потребовав наличие компакта, на к-ром лежат все осуществляющие гомологию цепи; определяем сходящийся цикл с компактным носителем. Обозначая индексом kвнизу переход к циклам и гомологиям с компактными носителями, приходим к группам
лежат в F. Аналогично изменим понятие гомологичности нулю цикла, потребовав наличие компакта, на к-ром лежат все осуществляющие гомологию цепи; определяем сходящийся цикл с компактным носителем. Обозначая индексом kвнизу переход к циклам и гомологиям с компактными носителями, приходим к группам  и
и  . Вторая из них наз. группой гомологии Вьеториса. В случае конечного полиэдра группы В. г. совпадают со стандартными.
. Вторая из них наз. группой гомологии Вьеториса. В случае конечного полиэдра группы В. г. совпадают со стандартными.
Определяются также относительные группы гомологии  по модулю подмножества
по модулю подмножества  . Именно,
. Именно,  -циклом множества Апо модулю Вназ. любая
-циклом множества Апо модулю Вназ. любая  -цепь
-цепь  в А, для к-рой цепь
в А, для к-рой цепь 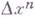 лежит в В. Аналогично,
лежит в В. Аналогично,  -цикл
-цикл 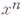 по модулю В
по модулю В  -гомологичен по модулю Внулю в А, если
-гомологичен по модулю Внулю в А, если 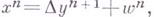 где
где  и
и  суть
суть 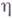 -цепи в А, и цепь
-цепи в А, и цепь 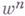 лежит в В.
лежит в В.
Лит.:[1] Александров П. С., Введение в гомологическую теорию размерности и общую комбинаторную топологию, М., 1975. А. А. Мальцев.

 в Ас условием
в Ас условием  После этого определяются
После этого определяются  -цепи множества Апо данной группе коэффициентов Gкак формальные конечные линейные комбинации
-цепи множества Апо данной группе коэффициентов Gкак формальные конечные линейные комбинации 
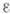 -симплексов
-симплексов  с коэффициентами
с коэффициентами  Граница
Граница 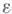 симплекса
симплекса  определяется так:
определяется так: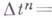
 это -
это -  -цепь. По линейности определяются граница любой
-цепь. По линейности определяются граница любой  -цепи, и
-цепи, и  -циклы как
-циклы как  -цепи с нулевой границей,
-цепи с нулевой границей,  -цепь
-цепь  множества
множества  -гомологична нулю в А (взаписи
-гомологична нулю в А (взаписи  ), если
), если  для нек-рой
для нек-рой  -цепи
-цепи  в А.
в А. в к-рой
в к-рой  есть
есть  -цикл в А, и
-цикл в А, и  . Истинные циклы образуют группу
. Истинные циклы образуют группу  (A, G). Истинный цикл z гомологичен нулю в А, если для любого
(A, G). Истинный цикл z гомологичен нулю в А, если для любого  существует такое N, что все
существует такое N, что все  при
при 
 -гомологичны нулю в А. Обозначим
-гомологичны нулю в А. Обозначим 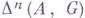 факторгруппу группы
факторгруппу группы 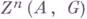 по подгруппе
по подгруппе  циклов, гомологичных нулю.
циклов, гомологичных нулю.  существует такое N, что любые два цикла
существует такое N, что любые два цикла  при
при  -гомологичны между собою в А. Обозначим группу сходящихся циклов
-гомологичны между собою в А. Обозначим группу сходящихся циклов 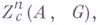 и пусть
и пусть  -соответствующая факторгруппа.
-соответствующая факторгруппа. , что все вершины всех симплексов всех циклов
, что все вершины всех симплексов всех циклов  лежат в F. Аналогично изменим понятие гомологичности нулю цикла, потребовав наличие компакта, на к-ром лежат все осуществляющие гомологию цепи; определяем сходящийся цикл с компактным носителем. Обозначая индексом kвнизу переход к циклам и гомологиям с компактными носителями, приходим к группам
лежат в F. Аналогично изменим понятие гомологичности нулю цикла, потребовав наличие компакта, на к-ром лежат все осуществляющие гомологию цепи; определяем сходящийся цикл с компактным носителем. Обозначая индексом kвнизу переход к циклам и гомологиям с компактными носителями, приходим к группам  и
и  . Вторая из них наз. группой гомологии Вьеториса. В случае конечного полиэдра группы В. г. совпадают со стандартными.
. Вторая из них наз. группой гомологии Вьеториса. В случае конечного полиэдра группы В. г. совпадают со стандартными. по модулю подмножества
по модулю подмножества  . Именно,
. Именно,  -циклом множества Апо модулю Вназ. любая
-циклом множества Апо модулю Вназ. любая  -цепь
-цепь  в А, для к-рой цепь
в А, для к-рой цепь 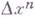 лежит в В. Аналогично,
лежит в В. Аналогично,  -цикл
-цикл 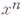 по модулю В
по модулю В  -гомологичен по модулю Внулю в А, если
-гомологичен по модулю Внулю в А, если 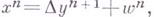 где
где  и
и  суть
суть 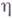 -цепи в А, и цепь
-цепи в А, и цепь 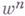 лежит в В.
лежит в В.