|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМЗначение ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ в математической энциклопедии: точно определенное указание действий над данными, позволяющее с помощью цифровой вычислительной машины дискретного действия преобразовать за конечное количество операций нек-рый массив данных (входные данные) в другой массив данных (выходные данные). В. а. реализуется в виде вычислительного процесса, т. е. в виде дискретно распределенной во времени конечной последовательности состояний реальной ЭВМ, имеющей, в отличие от абстрактной вычислительной машины, ограниченные скорость выполнения операций, разрядность чисел и объем памяти. При заданных ЭВМ и В. а. вычислительный процесс является строго детерминированным, т. е. заданным входным данным отвечают вполне определенным образом: последовательность операций ЭВМ; последовательность состояний ЭВМ; выходные данные. В. а. является линейным, если последовательность операций ЭВМ не зависит от входных данных, и нелинейным -в противном случае. Объектом операций ЭВМ являются данные, представляемые в виде машинных слов, интерпретируемых как машинные числа, машинные команды и т. п. Машинные числа обычно составляют конечное ограниченное множество Мчисел, размещенных в машинном интервале [ - А, А]и записанных в машинной разрядной сетке при заданном основании Машинная команда есть машинное слово, к-рое содержит информацию об операции, напр, арифметической, и ее оперантах (объектах, над к-рыми производится операция, и результате операции). Арифметич. операция над парой машинных чисел может вывести результат из совокупности Мпо двум причинам: вследствие превышения допустимого числа значащих цифр; вследствие превышения допустимой величины машинного числа. В первом случае применяется операция округления, к-рая возвращает результат действия в множество М, но делает само действие приближенным и приводит к потере точности. Второй случай приводит к аварийной остановке ЭВМ (АВОСТ, или "аварийный останов"). Композиция арифметич. операции, примененной к паре машинных чисел, и операции округления называется кваз и операцией. Множество Мвместе с определенной над ним совокупностью квазиопераций образует замкнутую систему N, однако, в отличие от поля действительных чисел, Nне образует поля. Система Nзависит от выбора ЭВМ. Реальный В. а. складывается из двух частей: а) абстрактного (или собственно) В. а., к-рый применяется к математич. объектам (элементам конечномерных векторных пространств, полей, алгебраич. систем, функциональных пространств и т. д.), не связан с конкретной ЭВМ и может записываться в общепринятых математич. терминах или ча каком-либо алгоритмич. языке; б) программы, т. е. совокупности машинных команд, описывающих В. а., к-рая организует реализацию вычислительного процесса в конкретной ЭВМ. Первая часть В. а. является исходной и переходит во вторую часть с помощью различных методов программирования. В. а. содержит ряд управляющих параметров, к-рые остаются неопределенными в первой части и фиксируются в программе, полностью определяя вычислительный процесс, обеспечивая адаптацию его первой части к конкретной ЭВМ. В. а. осуществляет переработку числовой и символьной информации и, как правило, связан с потерей информации и точности. Потеря точности является следствием ряда погрешностей, появляющихся на различных этапах вычислений: погрешности модели, аппроксимации, входных данных, округления. Погрешность модели является следствием приближенности математич. описания реального процесса. Погрешность входных данных зависит от ошибок наблюдения, измерения и т. п., но также может включать в себя и ошибку округления входной информации. Иногда погрешность модели и погрешность входных данных объединяют одним названием неустранимая погрешность. Погрешность аппроксимации возникает, если рассматривать абстрактный В. а. как нек-рую дискретную модель, к-рая, как правило, аппроксимирует континуальную модель. В нек-рых случаях абстрактный В. а. является самостоятельной дискретной моделью, к-рая не сопоставляется ни с какой другой моделью; в этом случае нет смысла говорить о погрешности аппроксимации. Погрешности округления могут встречаться только в реальном вычислительном процессе и зависят от выбора ЭВМ. При заданных входных данных и абстрактном В. а. промежуточные и выходные данные, получаемые в ЭВМ, зависят от выбора ЭВМ и режима ее работы (вычисления с одинарной и двойной точностью). Абстрактный В. а. допускает эквивалентные преобразования, к-рые при заданных входных данных могут менять промежуточные данные, но оставляют неизменным окончательный результат. В. а., соответствующий двум различным эквивалентным представлениям абстрактного В. а., может при фиксированной ЭВМ и входных данных приводить к различным окончательным результатам. Помимо свойства точности, В. а. должен обладать свойством устойчивости. Устойчивость В. а. определяется как свойство В. а., позволяющее судить о скорости накопления суммарной вычислительной погрешности. Имеется градация устойчивости (соответственно неустойчивости), основанная на измерении исходной ошибки округления и суммарной вычислительной погрешности в различных нормах. В тех случаях, когда В. а. сводится к последовательности линейных рекуррентных соотношений, устойчивость В. а. определяется в терминах норм конечномерных матриц в конечномерных векторных пространствах. Свойство устойчивости определяется как структурой абстрактного В. а., так и влиянием ошибок округления. Так, устойчивость итерационного процесса xn+1=Anxn+bn, где матрица А п также вычисляется, будет зависеть от влияния ошибок округления в коэффициентах матрицы на ее норму. Ошибки округления, входя в коэффициенты различных уравнений и операторов, вносят возмущения в математич. модель абстрактного В. а. и в этом смысле могут интерпретироваться так же, как и ошибки модели. Чем лучше свойства устойчивости абстрактного В. а., тем меньше, при заданном абстрактном В. а., результаты вычислений зависят от выбора ЭВМ и эквивалентных представлений абстрактного В. а. Другим условием, особенно важным в массовых вычислениях, является экономичность В. а., измеряемая затратой машинного времени, необходимой для достижения заданной точности вычисления. Экономичные В. а. получили широкое распространение в задачах математич. физики (см., напр., дробных шагов метод). Важной задачей теории В. а. является оптимизация В. а. При построении В. а. характерна тенденция к контролю точности. Контроль точности может косвенно осуществляться за счет увеличения устойчивости и порядка аппроксимации В. а., изменения параметров В. а. (внутренняя сходимость), сравнения двух численных решений одной и той же задачи, соответствующих различным В. а., применения тестов и т. д. Прямой контроль точности осуществляется в том случае, когда удается получить двусторонние оценки (или, по крайней мере, односторонние оценки) результата вычислений. Теоретич. оценки такого рода не всегда возможны и эффективны, т. к. не всегда дают достаточно точные границы отклонения численного решения от точного. Получил распространение интервальный анализ, к-рый дает возможность в процессе вычислений строить доверительные границы для вычисляемых величин. Различия в результатах абстрактного и реального В. а. определяются довольно сложными связями между их параметрами. Так, в абстрактном В. а. для сходящегося итерационного процесса точность е, вообще говоря, тем больше, чем больше число итераций п. В случае реального В. а. эта ситуация может измениться вследствие влияния ошибок округления и, начиная с нек-рого момента, разность между n-й итерацией и точным решением может потерять тенденцию к убыванию. Вообще говоря, абстрактный В. а. строится независимо от выбора конкретной ЭВМ и только косвенно учитывает ее конфигурацию своими свойствами аппроксимации и устойчивости. Так, для машин с большим быстродействием, но при малой оперативной памяти при решении дифференциальных уравнений с частными производными целесообразно применение экономичных абсолютно устойчивых схем высокой точности. В связи с появлением ЭВМ с параллельно действующими процессорами получили развитие параллельные алгоритмы и параллельное программирование. Сущность параллельного программирования заключается в разбиении перерабатываемых численных массивов на части (подмассивы), независимо перерабатываемые соответствующими процессорами; производится обмен информацией между подмассивами, причем время, затрачиваемое на этот обмен, существенно меньше, чем выигрыш времени, достигаемый в результате распараллеливания счета. Это делает эффективным применение ЭВМ с параллельным действием, позволяя достигать резкого увеличения быстродействия, особенно при решении больших задач. Многообразие ЭВМ приводит к многообразию программ, реализующих один и тот же абстрактный В. а. Составление программ является трудоемким процессом, и поэтому особое значение приобретает проблема адаптации, т. е. быстрого и по возможности автоматич. преобразования (при заданном абстрактном В. а.) программы с одной ЭВМ на другую (см. Программирование). Н. Н. Яненко. |
|
|
|

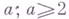 - нек-рое натуральное число, А - наибольшее машинное число (машинная бесконечность). Как следствие, машинные числа имеют ограничение по числу значащих цифр и по абсолютной величине. Конкретная ЭВМ может оперировать с различными множествами М, соответствующими различным основаниям, разрядным сеткам и машинным интервалам.
- нек-рое натуральное число, А - наибольшее машинное число (машинная бесконечность). Как следствие, машинные числа имеют ограничение по числу значащих цифр и по абсолютной величине. Конкретная ЭВМ может оперировать с различными множествами М, соответствующими различным основаниям, разрядным сеткам и машинным интервалам.