|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЫЧИСЛИМАЯ ФУНКЦИЯЗначение ВЫЧИСЛИМАЯ ФУНКЦИЯ в математической энциклопедии: функция, вычисление значений к-рой может быть проведено с помощью заранее заданной эффективной процедуры, или алгоритма. Характерная черта вычислительных процессов - вычисление искомых величин задач происходит последовательно из данных исходных величин по определенным, заранее заданным, правилам и инструкциям. На основании многочисленных примеров вычислительных процессов в математике оформилось интуитивное понятие вычислительной процедуры. В связи с общей программой обоснования математики в 20 в. возникла задача создания не интуитивного, а точного понятия алгоритма. Строгое определение В. ф., эффективных процедур и алгоритмов было дано в различных формах Д. Гильбертом (D. Hilbert), К. Гёделем (К. Godel), А. Чёрчем (A. Church), С. Клини (S. Kleene), Э. Постом (Е. Post), А. Тьюрингом (A. Turing) и А. А. Марковым. Общая идея различных подходов к созданию строгих математич. определений рассматриваемых понятий такова: проводится детальный анализ уже известных или мыслимых вычислительных процессов, выявляются существенные особенности этих процессов, находятся подходящие математич. аналоги этих процессов и их особенностей. Реализация различных аспектов этой идеи неоднозначна и приводит к разным вариантам мате-матич. понятия алгоритма. Основными математич. моделями понятия алгоритма являются машины Тьюринга, частично рекурсивные функции, нормальные алгоритмы Маркова и др. Машины Тьюринга. Алгоритмы, применяемые в математике, напоминают машину, работающую отдельными тактами и выдающую ответ через конечное число тактов. А. Тьюринг и Э. Пост описали понятия вычислительных машин абстрактных, на к-рых можно моделировать вычислительные процессы. Машина Тьюринга (иногда говорят машина Тьюринга - Поста) Мсостоит из: конечного алфавита конечного списка программы, составленной из отдельных команд Конфигурация машины Мв данный момент времени кодируется словом вида если D = Л, то получается слово если D=С, то получается слово если D = П и В = a р В', то получается слово если D = П и В - пустое слово, то получается слово Aaka0ql B. Работа машины Мможет быть описана следующим образом: кодируют исходные данные с помощью нек-рой начальной конфигурации (здесь Всякая вычислительная процедура, к-рая может быть сведена к работе подходящей машины Тьюринга, является эффективной в интуитивном смысле. Обращение предыдущего высказывания получило название т е-з и с а Тьюринга: всякая эффективная вычислительная процедура может быть реализована на соответствующей машине М. Этот тезис нельзя доказать, так как он объединяет два понятия - строгое математич. понятие машины Тьюринга и расплывчатое, интуитивное понятие эффективной процедуры. Если моделировать на машинах Тьюринга вычисление значений функции, области определения и значений к-рой суть множества натуральных чисел, то приходят к понятию вычислимой (на машинах Тьюринга) функции. См. также Тьюринга машина. Частично рекурсивные функции. Все известные примеры алгоритмов можно свести к вопросу вычисления значений подходящей функции. Считая эту черту алгоритмов основной, А. Чёрч, К. Гёдель и С. Клини выделили широкий класс функций, названных частично рекурсивными. Пусть F - класс частичных функций, области определения и значения к-рых суть множества натуральных чисел. На множестве Fопределяют следующие операции: суперпозиция функций: если получается из если Ясно, что если эти операции применяются к функциям, значение к-рых мы умеем вычислять, то имеются алгоритмы, вычисляющие значения функций Имеются легкие алгоритмы, вычисляющие значения простейших функций. Функция f наз. частично рекурсивной, если она за конечное число шагов может быть получена из простейших с помощью суперпозиции и Нормальные алгорифмы Маркова. Всякий конкретный алгоритм имеет дело с нек-рым алфавитом, и решение конкретной задачи сводится к переработке слов данного алфавита по нек-рым заранее заданным правилам. Такой подход к теории алгоритмов развит А. А. Марковым, предложившим концепцию нормального алгорифма в качестве математич. модели понятия вычислительной процедуры. Нормальный алгорифм j состоит из нек-рого алфавита Кодируя соответствующим образом информацию, можно использовать нормальные алгорифмы для решения разнообразных алгоритмич. задач. Всякая вычислительная процедура, промоделированная с помощью нормального алгорифма, является эффективной в интуитивном смысле. Обращение этого высказывания носит название тезиса Маркова: всякая эффективная вычислительная процедура может быть промоделирована с помощью подходящего нормального алгорифма. Если моделировать с помощью нормальных алгорифмов вычисление значений функций из класса F, то приходят к еще одному понятию вычислимой функции. Были предложены и другие уточнения понятия алгоритмов (см. Алгоритм, а также Нормальный алгорифм). Доказан следующий результат о равносильности различных концепций понятия алгоритма: классы функций, вычислимых на машинах Тьюринга, частично рекурсивных функций, вычислимых с помощью нормальных алгорифмов Маркова (аналогичные классы функций при других концепциях понятия алгоритма), совпадают. По мнению большинства современных математиков, этот класс функций адекватен классу интуитивно В. ф. и отождествляется с ним. Такое 1 отождествление позволяет придать математичность алгоритмическим проблемам. Лит.:[1] Мальцев А. И., Алгоритмы и рекурсивные функции, М., 1965; [2] Роджерс X., Теория рекурсивных функций и эффективная вычислимость, пер. с англ., М., 1972; [3] Тuring A. M., "Ргос. London Math. Soc.", 1937, v. 42, № 2, p. 230-65; [4] Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; [5] Марков А. А., Теория алгорифмов, М., 1954 ("Тр. матем. ин-та АН СССР", т. 42). И. А. Лавров, А. Д. Тайманов. |
|
|
|

 где
где 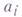 произвольные символы; конечные упорядоченные последовательности символов алфавита
произвольные символы; конечные упорядоченные последовательности символов алфавита  наз. словами в алфавите
наз. словами в алфавите 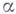 ; с помощью слов в алфавите
; с помощью слов в алфавите  кодируются исходные данные задачи, промежуточные вычисления и получаемые ответы;
кодируются исходные данные задачи, промежуточные вычисления и получаемые ответы;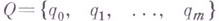 элементарных состояний, в к-рых машина Мможет находиться; при этом
элементарных состояний, в к-рых машина Мможет находиться; при этом  считается начальным состоянием, в к-ром находится М, когда начинает работу, а
считается начальным состоянием, в к-ром находится М, когда начинает работу, а 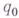 - конечным состоянием: если Мприходит в состояние
- конечным состоянием: если Мприходит в состояние 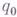 , то она останавливает свою работу;
, то она останавливает свою работу;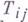 , имеющих один из видов:
, имеющих один из видов:  где
где 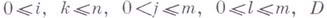 - один из символов движения Л, П или С.
- один из символов движения Л, П или С. где Аи В - нек-рые слова в алфавите
где Аи В - нек-рые слова в алфавите  (вместо пустого слова Апишут а 0). Конфигурация машины Мв следующий момент времени (после выполнения одного такта работы) также кодируется словом, к-рое зависит от команды :
(вместо пустого слова Апишут а 0). Конфигурация машины Мв следующий момент времени (после выполнения одного такта работы) также кодируется словом, к-рое зависит от команды :


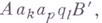
 ); согласно программе машины Мполучают следующую конфигурацию и т. д., если в какой-либо момент получают конфигурацию, содержащую конечное состояние
); согласно программе машины Мполучают следующую конфигурацию и т. д., если в какой-либо момент получают конфигурацию, содержащую конечное состояние 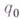 , то прекращают работу; заключительная конфигурация декодируется в ответ; если машина никогда не останавливается, то считают ответ в задаче неопределенным.
, то прекращают работу; заключительная конфигурация декодируется в ответ; если машина никогда не останавливается, то считают ответ в задаче неопределенным.
 то говорят, что функция
то говорят, что функция 
 с помощью суперпозиции; m-оператор: пусть
с помощью суперпозиции; m-оператор: пусть  говорят, что функция
говорят, что функция  получается из
получается из 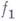 и
и  с помощью
с помощью 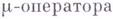 , и записывают
, и записывают 
 и
и  определены п неравны между собой при
определены п неравны между собой при  , а
, а 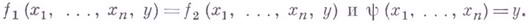
 и
и  Следующие функции считаются простейшими:
Следующие функции считаются простейшими:
 и
и 
 -оператора. Всюду определенная частично рекурсивная функция наз. общерекурсивной. Значение всякой частично рекурсивной функции может быть вычислено эффективно в интуитивном смысле. Обращение этого высказывания . получило название тезиса Чёрча: всякая функция, значение к-рой может вычисляться эффективно, является частично рекурсивной. Таким образом, согласно тезису Чёрча, вычислимыми функциями являются частично рекурсивные функции.
-оператора. Всюду определенная частично рекурсивная функция наз. общерекурсивной. Значение всякой частично рекурсивной функции может быть вычислено эффективно в интуитивном смысле. Обращение этого высказывания . получило название тезиса Чёрча: всякая функция, значение к-рой может вычисляться эффективно, является частично рекурсивной. Таким образом, согласно тезису Чёрча, вычислимыми функциями являются частично рекурсивные функции. и конечного упорядоченного списка правил вида
и конечного упорядоченного списка правил вида  , где
, где  - нек-рые слова в алфавите
- нек-рые слова в алфавите 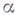 . Часть правил выделена и названа заключительными. Правило
. Часть правил выделена и названа заключительными. Правило  применяется к слову Рследующим образом: слово Рпредставляется в виде
применяется к слову Рследующим образом: слово Рпредставляется в виде 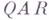 , где
, где 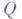 и
и  - слова в алфавите
- слова в алфавите  , возможно пустые, и из всех таких представлений выбирается то, в к-ром слово Qимеет наименьшую длину; тогда результатом применения данного правила к слову Рназ. слово QBR. Нормальный алгорифм
, возможно пустые, и из всех таких представлений выбирается то, в к-ром слово Qимеет наименьшую длину; тогда результатом применения данного правила к слову Рназ. слово QBR. Нормальный алгорифм  применяется к слову Рследующим образом: применяют к слову Рпервое правило из тех, к-рые к Рможно применить, получают слово
применяется к слову Рследующим образом: применяют к слову Рпервое правило из тех, к-рые к Рможно применить, получают слово 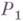 ; применяют к
; применяют к 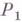 первое правило из тех, к-рые к
первое правило из тех, к-рые к 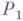 можно применить, получают слово
можно применить, получают слово 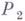 и т. д. В результате получается последовательность слов, к-рая обрывается после применения какого-либо заключительного правила.
и т. д. В результате получается последовательность слов, к-рая обрывается после применения какого-либо заключительного правила.