|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЫРОЖДЕННАЯ ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯЗначение ВЫРОЖДЕННАЯ ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ в математической энциклопедии: функция Куммера, функция Похгаммера,- решение вырожденного гипергеометрического уравнения В. г. ф. может быть определена с помощью так наз. ряда Куммера:
где наз. вырожденной гипергеометрической функцией 2-го рода. В. г. ф. В. г. ф. В. г. ф. Элементарные соотношения. Четыре функции Шесть формул такого типа могут быть получены из соотношений между смежными функциями для гипергео-метрич. функций. Последовательное применение этих рекуррентных формул приводит к линейным соотношениям, связывающим функцию Формула дифференцирования: Основные интегральные представления: Асимптотич. поведение В. г. ф. при Представления функций через В. г. ф. Функции Бесселя: Многочлены Лагерра: Интеграл вероятностей: Интегральная показательная функция: Интегральная логарифмическая функция: Гамма-функции: Элементарные функции: См. также [1], [2], [3], [8]. Лит,:[1] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции, [т. 2], пер. с англ.,2 изд., М., 1973; [2] Градштейн И. <С.,Рыжик И. М., Таблицы интегралов, сумм, рядов и произведений, 4 изд., М., 1963; [З] Handbook of mathematical functions with formulas, graphs and mathematical tables, N. Y., 1964; [4] Уиттекер Э.-Т., Ватсон Д.-Н., Курс современного анализа, ч. 2-Трансцендентные функции, пер. с англ., 2 изд., М., 1963; [5] Лебедев А. В., Федорова Р. М., Справочник по математическим таблицам, М., 1956; [6] Бурунова Н. М., Справочник по математическим таблицам, М., 1959; [71 An index of Mathematical tables, 2 ed , v. 1, 2, Oxford, 1962; [8] Лебедев Н. Н., Специальные функции и их приложения, 2 изд., М.-Л., 1963. 9. А. Чистова. |
|
|
|



 и
и  - параметры, принимающие любые действительные или комплексные значения, кроме
- параметры, принимающие любые действительные или комплексные значения, кроме 
 - комплексное переменное. Функция
- комплексное переменное. Функция 
 наз. вырожденной гипергеометрической функцией 1-го рода. Второе линейно независимое решение уравнения (1)
наз. вырожденной гипергеометрической функцией 1-го рода. Второе линейно независимое решение уравнения (1)
 - целая аналитич. функция во всей комплексной плоскости z; при фиксированном z - целая функция
- целая аналитич. функция во всей комплексной плоскости z; при фиксированном z - целая функция  и мероморфная функция g с простыми полюсами в точках
и мероморфная функция g с простыми полюсами в точках 
 - аналитич. функция в комплексной плоскости z с разрезом
- аналитич. функция в комплексной плоскости z с разрезом  и целая функция
и целая функция  и
и  .
. 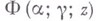 связана с гипергеометрической функцией
связана с гипергеометрической функцией  соотношением
соотношением 
 и
и  наз. смежными с функцией
наз. смежными с функцией  . Между
. Между  и любыми двумя смежными с ней существует линейная зависимость. Напр.,
и любыми двумя смежными с ней существует линейная зависимость. Напр.,
 с ассоциированными функциями
с ассоциированными функциями  где тип - целые числа.
где тип - целые числа.

 может быть изучено с помощью интегральных представлений (см. [1] - [3]). Если
может быть изучено с помощью интегральных представлений (см. [1] - [3]). Если  , в то время как
, в то время как  и
и  ограничены, то поведение функции
ограничены, то поведение функции  описывается формулой (2). В частности, при больших
описывается формулой (2). В частности, при больших  и ограниченных
и ограниченных  и
и  :
:






