"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЫПУКЛАЯ МЕТРИКАЗначение ВЫПУКЛАЯ МЕТРИКА в математической энциклопедии:
- внутренняя метрика на двумерном многообразии М, удовлетворяющая нек-рому условию выпуклости. Точнее, пусть lи m две кратчайшие, исходящие из нек-рой точки  , Xи Y - точки на них, х, у - расстояние от Одо X, Y, z - расстояние между , Xи Y - точки на них, х, у - расстояние от Одо X, Y, z - расстояние между 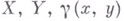 - угол в плоском треугольнике со сторонами, равными х, у, z, лежащий против стороны, равной z. Условие выпуклости метрики (в точке О).состоит в том, что - угол в плоском треугольнике со сторонами, равными х, у, z, лежащий против стороны, равной z. Условие выпуклости метрики (в точке О).состоит в том, что  является невозрастающей функцией (т. е. является невозрастающей функцией (т. е.  при при   ) на всякой паре промежутков ) на всякой паре промежутков  такой, что точки Xи Y, соответствующие любым двум значением из этих промежутков, можно соединить кратчайшей. Внутренняя метрика является В. м. тогда и только тогда, когда она есть метрика неотрицательной кривизны. Метрика выпуклой поверхности является В. м. Обратно, любое двумерное многообразие с В. м. реализуется в виде выпуклой поверхности (теорема А. Д. Александрова). такой, что точки Xи Y, соответствующие любым двум значением из этих промежутков, можно соединить кратчайшей. Внутренняя метрика является В. м. тогда и только тогда, когда она есть метрика неотрицательной кривизны. Метрика выпуклой поверхности является В. м. Обратно, любое двумерное многообразие с В. м. реализуется в виде выпуклой поверхности (теорема А. Д. Александрова).
Лит.:[1] Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М.-Л., 1948.
М. И. Войцеховский.
|

 , Xи Y - точки на них, х, у - расстояние от Одо X, Y, z - расстояние между
, Xи Y - точки на них, х, у - расстояние от Одо X, Y, z - расстояние между 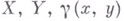 - угол в плоском треугольнике со сторонами, равными х, у, z, лежащий против стороны, равной z. Условие выпуклости метрики (в точке О).состоит в том, что
- угол в плоском треугольнике со сторонами, равными х, у, z, лежащий против стороны, равной z. Условие выпуклости метрики (в точке О).состоит в том, что  является невозрастающей функцией (т. е.
является невозрастающей функцией (т. е.  при
при 
 ) на всякой паре промежутков
) на всякой паре промежутков  такой, что точки Xи Y, соответствующие любым двум значением из этих промежутков, можно соединить кратчайшей. Внутренняя метрика является В. м. тогда и только тогда, когда она есть метрика неотрицательной кривизны. Метрика выпуклой поверхности является В. м. Обратно, любое двумерное многообразие с В. м. реализуется в виде выпуклой поверхности (теорема А. Д. Александрова).
такой, что точки Xи Y, соответствующие любым двум значением из этих промежутков, можно соединить кратчайшей. Внутренняя метрика является В. м. тогда и только тогда, когда она есть метрика неотрицательной кривизны. Метрика выпуклой поверхности является В. м. Обратно, любое двумерное многообразие с В. м. реализуется в виде выпуклой поверхности (теорема А. Д. Александрова).