|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯЗначение ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ в математической энциклопедии: незатухающие колебания в к.-л. материальной системе, возникающие под действием внешней переменной во времени силы. В линейной диссипативной системе при действии на нее внешней силы, изменяющейся по гармоническому закону, В. к. имеют частоту внешней силы. Амплитуда В. к. определяется параметрами внешнего воздействия (амплитудой, частотой) и коэффициентами сопротивления среды, в к-рой происходят колебания материальной системы. Если частота внешней силы близка к одной из частот собственных колебаний системы, то амплитуда В. к. может иметь достаточно большую величину, тем большую, чем меньше сопротивление среды. В случае отсутствия сопротивления среды при совпадении частоты внешней силы с одной из частот собственных колебаний системы амплитуда В. к. неограниченно возрастает пропорционально времени. Это явление носит название резонанса. При включении внешней силы в материальной системе возникают как В. к., так и собственные колебания. В диссипативной системе собственные колебания затухают, и в системе остаются только В. к. (установившийся р е ж и м). Режим перехода к установившимся колебаниям наз. переходным режимом. Время переходного режима тем меньше, чем больше сопротивление среды. Если внешняя сила является периоднч. функцией времени с периодом Если при к.-л. значении пчастота пр близка к одной из собственных частот системы, то амплитуда гармоники В. к. с частотой пр может быть достаточно большой, а при отсутствии сопротивления среды будет расти пропорционально времени. Напр., для диссипативной системы с одной степенью свободы, уравнение движения к-рой имеет вид ( где где значок (s)у суммы означает, что член при n=s в сумму не входит. При непериодическом внешнем возмущении возникающие в системе В. к. будут также непериодическими. При воздействии внешней гармонической силы на нелинейную диссипативную систему возможно возникновение В. к. не только с частотой внешней силы, но н с частотой, в целое число раз большей частоты внешней силы (субгармонические колебания). В автоколебательной системе (см. Автоколебания).при действии на нее внешней гармонической силы возникает квазипериодический режим (режим биений), характеризующийся наличием периодич. колебания с частотой, близкой к частоте автоколебаний, и В. к. с частотой внешнего возмущения. При частоте внешнего возмущения, близкой к частоте автоколебаний, система совершает колебания только с частотой внешней силы. Это явление носит назв. п р и-пуд и тельной синхронизации (захватывание). Лит.:[1] Андронов А. А., Собрание трудов, [М.], 1956; [2] Бабаков И. М., Теория колебаний, 2 изд., М., 1365; [3] Бутени н Н. В., Теория колебаний, 2 изд., М., 1963; [4] Коловский М. 3., Нелинейная теория виброзащитных систем, М., 1966; [5] Стокер Д ж., Нелинейные колебания в механических и электрических системах, пер. с англ., 2 изд., М., 1953; [6] Стрелков С. П., Введение в теорию колебаний, 2 изд.. М., 1964; [7] Цзе Ф. С., Морзе И. Е., X инк л Р. Т., Механические колебания, пер. с англ., М., 1966. Н. В. Бутенин. |
|
|
|

 , к-рая может быть представлена рядом Фурье, то в линейной системе возникают В. к., представляющие собой сумму гармоник с частотами
, к-рая может быть представлена рядом Фурье, то в линейной системе возникают В. к., представляющие собой сумму гармоник с частотами  . Амплитуды этих гармоник убывают с возрастанием n, но не равномерно. На практике часто ограничиваются конечным числом гармоник.
. Амплитуды этих гармоник убывают с возрастанием n, но не равномерно. На практике часто ограничиваются конечным числом гармоник.
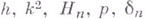 - постоянные коэффициенты), В. к. будут происходить по закону
- постоянные коэффициенты), В. к. будут происходить по закону 
 . Если же
. Если же  (среда без сопротивления) и
(среда без сопротивления) и  , то
, то 