|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЫВОДЗначение ВЫВОД в математической энциклопедии: логический - формальный вывод в исчислении, содержащем логические правила и имеющем в качестве основных выводимых объектов формулы (интерпретацией к-рых являются суждения;см. Логические исчисления. Логико-математические исчисления). Поскольку обычно такие исчисления снабжаются семантикой, то в некоторых случаях под логическим В. понимают содержательное рассуждение, позволяющее от сформулированных аксиом и гипотез (допущений) переходить к новым утверждениям, логически вытекающим из исходных. При зафиксированных аксиомах и правилах логических переходов (см. Вывода правило).говорят, что последовательность формул является выводом (своего последнего члена А).из гипотез Формирование понятия В. (и систем, в терминах к-рых это понятие получает смысл) знаменовало собой возникновение современной математич. логики. Новое, более строгое понимание аксиоматич. метода, при к-ром формализации подлежат не только аксиомы, но и логические средства, открыло возможность математич. определения понятия доказательства и изучения доказательств математнч. методами (см. Доказательств теория). Поня-. тие формального В. оказалось хорошим приближением к понятию математич. истины (см. Гёделя теорема о полноте, Гёделя теорема о неполноте). Искусственная формализация понятия логической выводимости в дальнейшем существенно сблизилась с реальными способами содержательного математич. рассуждения (см. Естественный логический вывод). Лит.:[1] Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; [2] Математическая теория логического вывода, сб. переводов, М., 1967. С. Ю. Маслов. |
|
|
|


 , если каждый член последовательности либо является аксиомой или одной из гипотез, либо получается из предыдущих формул последовательности по одному из правил. Это записывается в виде
, если каждый член последовательности либо является аксиомой или одной из гипотез, либо получается из предыдущих формул последовательности по одному из правил. Это записывается в виде  при этом формула Аназ. выводимой из A1,..., An. В случае n=0 запись
при этом формула Аназ. выводимой из A1,..., An. В случае n=0 запись  означает, что Авыводимо в рассматриваемом исчислении без к.-л. допущений; применяется также запись
означает, что Авыводимо в рассматриваемом исчислении без к.-л. допущений; применяется также запись 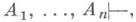 означающая, что "допущения
означающая, что "допущения  ведут к противоречию" (в большинстве изучавшихся систем
ведут к противоречию" (в большинстве изучавшихся систем  влечет выводимость из этих гипотез любой формулы). Напр., в исчислении, содержащем аксиому
влечет выводимость из этих гипотез любой формулы). Напр., в исчислении, содержащем аксиому  и правило модус поненс, последовательность
и правило модус поненс, последовательность 
 является выводом
является выводом  из
из  Свойствами логической выводимости являются:
Свойствами логической выводимости являются: если
если  если
если  если
если 
 (здесь Аи В - формулы, Г и Г'- списки формул,
(здесь Аи В - формулы, Г и Г'- списки формул,  - формула или пустое слово). Эти свойства позволяют существенно преобразовывать списки гипотез и, наряду с правилами введения и удаления логических символов (см. Выводимое правило), сближают системы со знаком
- формула или пустое слово). Эти свойства позволяют существенно преобразовывать списки гипотез и, наряду с правилами введения и удаления логических символов (см. Выводимое правило), сближают системы со знаком  с Генцена формальными системами. Для исчислений, основанных на классич. логике, характерно свойство
с Генцена формальными системами. Для исчислений, основанных на классич. логике, характерно свойство  . Для, интуиционистской логики (конструктивной логики) в широких предположениях удается доказывать принципы брауэровского понимания выводимости: 1) если
. Для, интуиционистской логики (конструктивной логики) в широких предположениях удается доказывать принципы брауэровского понимания выводимости: 1) если  , то имеет место одна из вы-водимостей
, то имеет место одна из вы-водимостей  или
или  ; 2) если
; 2) если  , то, для некоторого терма t,
, то, для некоторого терма t, . (упомянутые предположения во всяком случае выполнены при пустом Г). Возможности избавления от допущений, включая переход к выводам без гипотез, регулируются дедукции теоремой.
. (упомянутые предположения во всяком случае выполнены при пустом Г). Возможности избавления от допущений, включая переход к выводам без гипотез, регулируются дедукции теоремой.