|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВПОЛНЕ ХАРАКТЕРИСТИЧЕСКАЯ КОНГРУЭНЦИЯЗначение ВПОЛНЕ ХАРАКТЕРИСТИЧЕСКАЯ КОНГРУЭНЦИЯ в математической энциклопедии: - конгруэнция В. х. к. алгебраич. системы Аобразуют по включению полную подрешетку Лит.:[1] Мальцев А. И., Алгебраические системы, М., 1970. Д. М. Смирнов. ВПОЛНЕ ХАРАКТЕРИСТИЧЕСКАЯ ПОДГРУППА- подгруппа группы G, инвариантная относительно всех эндоморфизмов группы G. Совокупность всех В. х. л. образует подрешетку в решетке всех подгрупп группы. Коммутант и члены нижнего центрального ряда являются В. х. п. в произвольной группе. Более того, любая вербальная подгруппа группы есть В. х. п. Для свободных групп верно и обратное: любая В. х. п. является вербальной. Лит.: [1] Магнус В., Каррас А., Солитэр Д., Комбинаторная теория групп, пер. с англ.. М., 1974. В. Н. Ремесленников. |
|
|
|

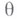 алгебраической системы
алгебраической системы
 , к-рая выдерживает любой эндоморфизм а этой системы, т. е. из
, к-рая выдерживает любой эндоморфизм а этой системы, т. е. из  следует
следует 
 решетки
решетки 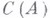 всех конгруэнции системы А. Если
всех конгруэнции системы А. Если  - многообразие
- многообразие  -систем и F - свободная в
-систем и F - свободная в 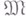 система счетного ранга, то решетка
система счетного ранга, то решетка  В. х. к. системы Fинверсно изоморфна решетке
В. х. к. системы Fинверсно изоморфна решетке  всех подмногообразий многообразия
всех подмногообразий многообразия  . Всякая конгруэнция
. Всякая конгруэнция 
 -алгебры Ас конечным числом порождающих, имеющая конечный индекс в А(т. е. конечное число смежных классов
-алгебры Ас конечным числом порождающих, имеющая конечный индекс в А(т. е. конечное число смежных классов  .), содержит В. х. к.
.), содержит В. х. к. алгебры А, также имеющую конечный индекс в А.
алгебры А, также имеющую конечный индекс в А.