"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
l-АДИЧЕСКИЕ КОГОМОЛОГИИЗначение l-АДИЧЕСКИЕ КОГОМОЛОГИИ в математической энциклопедии:
- одна из конструкций когомологий абстрактных алгебраич. многообразий и схем. Этальные когомологий схем являются пе-риодич. модулями. Для различных нужд, в первую очередь для доказательства формулы Лефшеца и приложений к дзета-функциям, необходимы когомологий "с коэффициентами в кольцах нулевой характеристики". Они получаются из этальных когомологий переходом к проективному пределу.
Пусть l - простое число, l-адическим пучком на схеме Xназ. проективная система 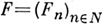 этальных абелевых пучков этальных абелевых пучков 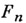 такая, что для всех и гомоморфизмы перехода такая, что для всех и гомоморфизмы перехода  эквивалентны кано-нич. морфизму эквивалентны кано-нич. морфизму  Каждая компонента Р пZ-адического пучка является пучком Каждая компонента Р пZ-адического пучка является пучком  Z- модулей. Z-адический пучок Fназ. конструктивным (соответственно, локально постоянным), если все пучки Z- модулей. Z-адический пучок Fназ. конструктивным (соответственно, локально постоянным), если все пучки  конструктивные (локально постоянные) этальные пучки. Имеет место естественная эквивалентность категории локально постоянных конструктивных пучков на связной схеме Xи категорией модулей конечного типа над кольцом конструктивные (локально постоянные) этальные пучки. Имеет место естественная эквивалентность категории локально постоянных конструктивных пучков на связной схеме Xи категорией модулей конечного типа над кольцом  целых Z-адических чисе. <л, на к-рых непрерывно слева действует фундаментальная группа схемы X. Это показывает, что конструктивные локально постоянные пучки являются абстрактными аналогами системы локальных коэффициентов в топологии. Примерами конструктивных l-адических пучков являются пучок целых Z-адических чисе. <л, на к-рых непрерывно слева действует фундаментальная группа схемы X. Это показывает, что конструктивные локально постоянные пучки являются абстрактными аналогами системы локальных коэффициентов в топологии. Примерами конструктивных l-адических пучков являются пучок  пучки Тейта пучки Тейта 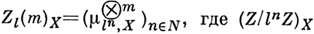 - постоянный пучок на X, ассоциированный с группой - постоянный пучок на X, ассоциированный с группой 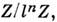 а а 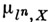 - пучок корней - пучок корней 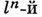 степени из единицы на X. Если А - абелева схема над X, то степени из единицы на X. Если А - абелева схема над X, то  , где , где  - ядро умножения в A на - ядро умножения в A на 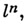 образует локально постоянный конструктивный l-адический пучок на X, наз. модулем Тейта абелевой схемы А. Если X - схема над полем k,a образует локально постоянный конструктивный l-адический пучок на X, наз. модулем Тейта абелевой схемы А. Если X - схема над полем k,a 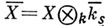 - схема, полученная из Xзаменой базы с kна сепарабельное замыкание - схема, полученная из Xзаменой базы с kна сепарабельное замыкание 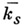 поля поля 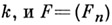 - l-адический пучок на X, то этальные когомологий - l-адический пучок на X, то этальные когомологий 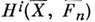 определяют проективную систему определяют проективную систему  -модулей. Проективный предел -модулей. Проективный предел 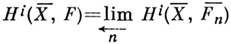 естественным образом снабжается структурой естественным образом снабжается структурой 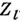 -модуля, на к-ром -модуля, на к-ром  действует непрерывно относительно l-адической топологии, и наз. i-ми l-адическими когомологиями пучка действует непрерывно относительно l-адической топологии, и наз. i-ми l-адическими когомологиями пучка 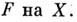 В случае, когда В случае, когда 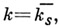 обычно пишут обычно пишут  На На 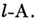 к. конструктивных l-адических пучков переносятся фундаментальные теоремы об этальных когомологиях. Если к. конструктивных l-адических пучков переносятся фундаментальные теоремы об этальных когомологиях. Если 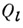 - поле рациональных l-адических чисел, то - поле рациональных l-адических чисел, то 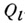 -пространства -пространства  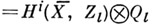 наз. рациональными l-адическими когомологиями схемы X. Их размерность наз. рациональными l-адическими когомологиями схемы X. Их размерность  (в случае, когда она определена) наз. i-м числом Бетти X. Для полных k-схем числа bi(X;l).определены и не зависят от (в случае, когда она определена) наз. i-м числом Бетти X. Для полных k-схем числа bi(X;l).определены и не зависят от  Если k - алгебраически замкнутое поле характеристики Если k - алгебраически замкнутое поле характеристики 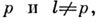 то сопоставление гладкому полному k- многообразию пространств то сопоставление гладкому полному k- многообразию пространств  определяет Вейля когомологий. В случае, когда k=C - поле комплексных чисел, имеет место теорема сравнения: определяет Вейля когомологий. В случае, когда k=C - поле комплексных чисел, имеет место теорема сравнения:  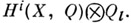 Лит.:[1] Grothendieck А., в кн.: Seminare Bourbaki, Textes des conferences. Annee, 1964/65, N.Y.-Amst., Лит.:[1] Grothendieck А., в кн.: Seminare Bourbaki, Textes des conferences. Annee, 1964/65, N.Y.-Amst.,
1966, exposes Ns279, p. 1 - 15. И. В. Долгачев.
|

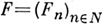 этальных абелевых пучков
этальных абелевых пучков 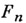 такая, что для всех и гомоморфизмы перехода
такая, что для всех и гомоморфизмы перехода  эквивалентны кано-нич. морфизму
эквивалентны кано-нич. морфизму  Каждая компонента Р пZ-адического пучка является пучком
Каждая компонента Р пZ-адического пучка является пучком  Z- модулей. Z-адический пучок Fназ. конструктивным (соответственно, локально постоянным), если все пучки
Z- модулей. Z-адический пучок Fназ. конструктивным (соответственно, локально постоянным), если все пучки  конструктивные (локально постоянные) этальные пучки. Имеет место естественная эквивалентность категории локально постоянных конструктивных пучков на связной схеме Xи категорией модулей конечного типа над кольцом
конструктивные (локально постоянные) этальные пучки. Имеет место естественная эквивалентность категории локально постоянных конструктивных пучков на связной схеме Xи категорией модулей конечного типа над кольцом  целых Z-адических чисе. <л, на к-рых непрерывно слева действует фундаментальная группа схемы X. Это показывает, что конструктивные локально постоянные пучки являются абстрактными аналогами системы локальных коэффициентов в топологии. Примерами конструктивных l-адических пучков являются пучок
целых Z-адических чисе. <л, на к-рых непрерывно слева действует фундаментальная группа схемы X. Это показывает, что конструктивные локально постоянные пучки являются абстрактными аналогами системы локальных коэффициентов в топологии. Примерами конструктивных l-адических пучков являются пучок  пучки Тейта
пучки Тейта 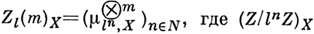 - постоянный пучок на X, ассоциированный с группой
- постоянный пучок на X, ассоциированный с группой 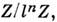 а
а 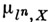 - пучок корней
- пучок корней 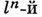 степени из единицы на X. Если А - абелева схема над X, то
степени из единицы на X. Если А - абелева схема над X, то  , где
, где  - ядро умножения в A на
- ядро умножения в A на 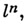 образует локально постоянный конструктивный l-адический пучок на X, наз. модулем Тейта абелевой схемы А. Если X - схема над полем k,a
образует локально постоянный конструктивный l-адический пучок на X, наз. модулем Тейта абелевой схемы А. Если X - схема над полем k,a 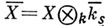 - схема, полученная из Xзаменой базы с kна сепарабельное замыкание
- схема, полученная из Xзаменой базы с kна сепарабельное замыкание 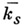 поля
поля 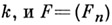 - l-адический пучок на X, то этальные когомологий
- l-адический пучок на X, то этальные когомологий 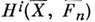 определяют проективную систему
определяют проективную систему  -модулей. Проективный предел
-модулей. Проективный предел 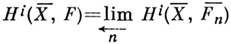 естественным образом снабжается структурой
естественным образом снабжается структурой 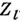 -модуля, на к-ром
-модуля, на к-ром  действует непрерывно относительно l-адической топологии, и наз. i-ми l-адическими когомологиями пучка
действует непрерывно относительно l-адической топологии, и наз. i-ми l-адическими когомологиями пучка 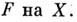 В случае, когда
В случае, когда 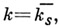 обычно пишут
обычно пишут  На
На 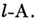 к. конструктивных l-адических пучков переносятся фундаментальные теоремы об этальных когомологиях. Если
к. конструктивных l-адических пучков переносятся фундаментальные теоремы об этальных когомологиях. Если 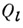 - поле рациональных l-адических чисел, то
- поле рациональных l-адических чисел, то 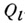 -пространства
-пространства 
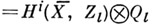 наз. рациональными l-адическими когомологиями схемы X. Их размерность
наз. рациональными l-адическими когомологиями схемы X. Их размерность  (в случае, когда она определена) наз. i-м числом Бетти X. Для полных k-схем числа bi(X;l).определены и не зависят от
(в случае, когда она определена) наз. i-м числом Бетти X. Для полных k-схем числа bi(X;l).определены и не зависят от  Если k - алгебраически замкнутое поле характеристики
Если k - алгебраически замкнутое поле характеристики 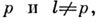 то сопоставление гладкому полному k- многообразию пространств
то сопоставление гладкому полному k- многообразию пространств  определяет Вейля когомологий. В случае, когда k=C - поле комплексных чисел, имеет место теорема сравнения:
определяет Вейля когомологий. В случае, когда k=C - поле комплексных чисел, имеет место теорема сравнения: 
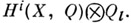 Лит.:[1] Grothendieck А., в кн.: Seminare Bourbaki, Textes des conferences. Annee, 1964/65, N.Y.-Amst.,
Лит.:[1] Grothendieck А., в кн.: Seminare Bourbaki, Textes des conferences. Annee, 1964/65, N.Y.-Amst.,