|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВОССТАНОВЛЕНИЯ ТЕОРИЯЗначение ВОССТАНОВЛЕНИЯ ТЕОРИЯ в математической энциклопедии: - раздел теории вероятностей, описывающий широкий круг явлений, связанных с отказом и восстановлением элементов какой-либо системы. Основные понятия в В. т.- понятия процесса восстановления и уравнения восстановления. Процесс восстановления описывается с помощью классич. схемы сумм независимых случайных величин следующим образом. Пусть
Если В случае, когда и Процесс восстановления где Имеются многочисленные результаты, обобщающие и уточняющие (3) и (4) в различных направлениях. С помощью результатов типа (3) и (4) изучаются асимптотич. свойства решения Х(t) уравнения типа восстановления: в к-ром свободный член K(t).есть нек-рая функция, отличная от F(t).и удовлетворяющая тем или иным условиям. Из определения (1) вытекает соотношение Поскольку предельные теоремы для сумм Имеется большое количество обобщений изложенной выше схемы. Одно из таких обобщений, связанное с полумарковскими процессами, дает так наз. марковский процесс восстановления, в к-ром система имеет какое-то количество состояний и времена работы отдельных элементов являются случайными величинами, зависящими от состояний системы до и после момента восстановления. Лит.:[1]Кокc Д. Р., Смит В. Л., Теория восстановления, пер. с англ., М., 1967. Б. А. Севастьянов. |
|
|
|

 - последовательность независимых, неотрицательных, одинаково распределенных случайных величин с функцией распределения F(x). Пусть
- последовательность независимых, неотрицательных, одинаково распределенных случайных величин с функцией распределения F(x). Пусть 
 . Процесс восстановления
. Процесс восстановления  определяется следующим образом
определяется следующим образом
 интерпретировать как длительности работы к.-л. последовательно заменяемых элементов, то случайная величина Nt равна числу замен (или восстановлений) этих элементов за время t. При исследовании
интерпретировать как длительности работы к.-л. последовательно заменяемых элементов, то случайная величина Nt равна числу замен (или восстановлений) этих элементов за время t. При исследовании  большую роль играет функция восстановления
большую роль играет функция восстановления  . Эта функция удовлетворяет уравнению восстановления:
. Эта функция удовлетворяет уравнению восстановления: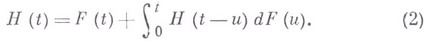
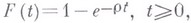 имеет место важный частный случай процесса восстановления - пуассоновский процесс, в к-ром
имеет место важный частный случай процесса восстановления - пуассоновский процесс, в к-ром 

 и уравнение восстановления (2) имеют большое значение при исследовании различных задач как прикладного, так и теоретич. характера в теории массового обслуживания, в теории надежности, в теории запасов, в теории ветвящихся, процессов и т. п. Значительное количество результатов в В. т. связано с изучением асимптотических при
и уравнение восстановления (2) имеют большое значение при исследовании различных задач как прикладного, так и теоретич. характера в теории массового обслуживания, в теории надежности, в теории запасов, в теории ветвящихся, процессов и т. п. Значительное количество результатов в В. т. связано с изучением асимптотических при  свойств функции восстановления
свойств функции восстановления  . В элементарной теореме восстановления утверждается, что
. В элементарной теореме восстановления утверждается, что 
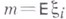 . Д. Блэкуэлл (D. Blackwell, 1948) доказал (см. [1]), что в случае, если распределение
. Д. Блэкуэлл (D. Blackwell, 1948) доказал (см. [1]), что в случае, если распределение  не сосредоточено на к.-л. арпфметич. решетке вида
не сосредоточено на к.-л. арпфметич. решетке вида  d>0, то при любом h>0
d>0, то при любом h>0

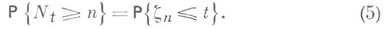
 независимых слагаемых хорошо изучены, то соотношение (5) позволяет получать предельные теоремы для числа восстановлений Nt.
независимых слагаемых хорошо изучены, то соотношение (5) позволяет получать предельные теоремы для числа восстановлений Nt.