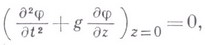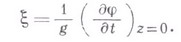|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВОЛНЫЗначение ВОЛНЫ в математической энциклопедии: на поверхности жидкости - отклонения поверхности жидкости от равновесного состояния, распространяющиеся под действием сил, стремящихся восстановить это состояние. В зависимости от природы восстанавливающих равновесие сил: поверхностного натяжения или тяжести, В. на поверхности жидкости подразделяются соответственно на капиллярные и гравитационные В. Теория гравитационных В. наиболее полно развита для потенциальных движении жидкости и особенно для плоскопараллельных движений; объемные силы, приложенные к частицам жидкости, суть силы тяжести. Определение потенциала скорости волнового движения требует интегрирования уравнения Лапласа:
к-рое должно соблюдаться при Кроме этих условий, должно быть удовлетворено требование обтекания поверхности твердых тел, находящихся в потоке. Одновременно с граничными условиями должны удовлетворяться начальные условия, к-рые состоят в том, что при t=0 частицы жидкости должны иметь предписываемые им начальные скорости, а поверхность жидкости - выбранную для нее начальную форму. Это равноценно заданию потенциала скоростей при t=0 как функции х, у, z и заданию функции Главная трудность задачи состоит в том, что все перечисленные условия необходимо должны выполняться на поверхности Почти полная невозможность решения задач теории В. с точным соблюдением указанных граничных условий привела к возникновению теории бесконечно малых В. В этой теории предполагается, что скорости частиц жидкости и отклонения поверхности жидкости от равновесного горизонтального уровня есть величины малые. В этом предположении граничные условия (1) и (2) принимают следующий вид:
Вместе с тем допускается возможность заменить в частных производных потенциала скоростей переменное
уравнение волновой поверхности - вид" Основные результаты, полученные в теории бесконечно малых В., дали возможность разобрать многие важные задачи геофизики и выяснить, напр., законы распространения приливных В. на поверхности Мирового-океана. Теория бесконечно малых В. нашла приложение к решению задач об образовании В. движущимися судами и дала возможность построить гидродинамич. теорию качки судов на волнении. Широкое применение методов теории функций комплексного переменного позволило решить ряд весьма сложных задач о распространении В. в бассейнах переменной глубины и рассмотреть вопросы, связанные с дифракцией и отражением В. от плавающих тел. Теория В. конечной амплитуды развита в работах А. И. Некрасова (см. [3]), к-рые дали возможность найти вид периодических В. в предположениях плоской задачи с точным удовлетворением граничных условий (1) и (2). Определение соответствующего потенциала скоростей было сведено к отысканию функции, устанавливающей конформное отображение области, занятой одной В., на круг или на область, ограниченную двумя концентрич. окружностями. Эта функция находится из решения нек-рого нелинейного интегрального уравнения. С развитием теории нелинейных граничных задач и интегральных уравнений теория В. конечной амплитуды обогатилась новыми результатами. В частности, было дано доказательство существования одиночной В. и предельной волны Стокса с угловой точкой на ее профиле. В теории стоячих В. конечной амплитуды, то есть периодических собственных колебаний поверхности жидкости, существуют лишь приближенные решения, основанные на применении переменных Лагранжа. Определение стоячих и установившихся В. на поверхности трехмерного потока представляет трудную задачу даже при отыскании ее приближенного решения. Лит.: [1] Ламб Г., Гидродинамика, пер. с англ., М.-Л., 1947; [2] Милн -Томсон Л. М., Теоретическая гидродинамика, пер. с англ., М., 1964; [3] Некрасов А. И., Собр. соч., т. 1, М., 1961, с. 358-439; [4] Стокер Дж. Дж., Волны на воде, пер. с англ., М., 1959; [5] Теория поверхности ных волн, сб. переводов, М., 1959. Л. Н. Сретенский. |
|
|
|

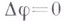 при граничных условиях особого вида. Вдоль всей поверхности жидкости, уравнение к-рой
при граничных условиях особого вида. Вдоль всей поверхности жидкости, уравнение к-рой 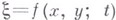 может быть найдено после решения задачи, давление постоянно. Это приводит на основании известного интеграла уравнений гидродинамики к первому граничному условию
может быть найдено после решения задачи, давление постоянно. Это приводит на основании известного интеграла уравнений гидродинамики к первому граничному условию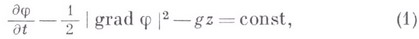
 . Второе граничное условие следует из того, что во все время движения поверхность жидкости состоит из одних и тех же частиц. Именно, при
. Второе граничное условие следует из того, что во все время движения поверхность жидкости состоит из одних и тех же частиц. Именно, при  :
: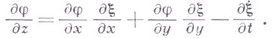 (2)
(2)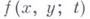 при t=0.
при t=0.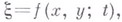 уравнение к-рой может быть найдено лишь после решения самой задачи. В этом отношении задачи теории В. имеют много общего с задачами теории струй и фигур равновесия вращающейся жидкости.
уравнение к-рой может быть найдено лишь после решения самой задачи. В этом отношении задачи теории В. имеют много общего с задачами теории струй и фигур равновесия вращающейся жидкости.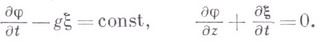
 нулем. При таком допущении граничное условие для функции
нулем. При таком допущении граничное условие для функции 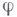 получает вид:
получает вид: