|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВОЛНОВОЕ УРАВНЕНИЕЗначение ВОЛНОВОЕ УРАВНЕНИЕ в математической энциклопедии: уравнение с частными производными вида описывающее различные колебательные процессы и процессы распространения волн. Для В. у., являющегося уравнением гиперболич. типа, обычно ставятся две задачи: Коши задача и смешанная задача. Классич. решением задачи Коши, описывающей распространение волн в n-мерном евклидовом пространстве Е", наз. функцию где Классич. решением смешанной задачи, описывающей колебания ограниченного объема
и удовлетворяет к.-л. краевому условию на "боковой" поверхности указанного цилиндра. Классич. решение задачи Коши для достаточно гладких Наряду с изучением указанных задач в приведенной выше классич. постановке рассматриваются вопросы существования и единственности классич. решений, понимаемых в более слабом смысле (см. [4]), а также обобщенных решений как задачи Коши, так и смешанной задачи (см. [2], [3]). Лит.:[1] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М.. 1966; [2] Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; [3] Ладыженская О. А., Смешанная задача для гиперболического уравнения, М., 1953; [4] Ильин В. А., "Успехи матем. наук", 1960, т. 15, в. 2 (92), с. 97-154; [5] Соболев С. Л., Некоторые применения функционального анализа в математической физике, Новосиб., 1962. Ш. А. Алимов. |
|
|
|

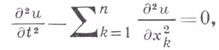
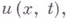 к-рая: непрерывно дифференцируема в
к-рая: непрерывно дифференцируема в  -мерном полупространстве (
-мерном полупространстве (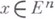 ,
,  ); дважды непрерывно дифференцируема и удовлетворяет В. у. в полупространстве (
); дважды непрерывно дифференцируема и удовлетворяет В. у. в полупространстве ( ); удовлетворяет начальным условиям
); удовлетворяет начальным условиям 
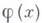 и
и 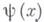 - заданные функции.
- заданные функции. , наз. функцию
, наз. функцию 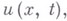 к-рая: непрерывно дифференцируема в замкнутом цилиндре
к-рая: непрерывно дифференцируема в замкнутом цилиндре 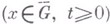 ; дважды непрерывно дифференцируема и удовлетворяет В. у. в открытом цилиндре
; дважды непрерывно дифференцируема и удовлетворяет В. у. в открытом цилиндре 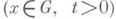 ; удовлетворяет для
; удовлетворяет для  начальным условиям
начальным условиям 
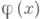 и
и 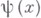 дается так наз. Пуассона формулой, к-рая при n=1 переходит в Д'Аламбера формулу. В случае, когда в правой части В. у. вместо нуля стоит заданная функция
дается так наз. Пуассона формулой, к-рая при n=1 переходит в Д'Аламбера формулу. В случае, когда в правой части В. у. вместо нуля стоит заданная функция 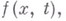 это уравнение наз. неоднородным В. у. и решение его дается так наз. Кирхгофа формулой. Смешанная задача для В. у. решается методом Фурье, методом конечных разностей и методом преобразования Лапласа.
это уравнение наз. неоднородным В. у. и решение его дается так наз. Кирхгофа формулой. Смешанная задача для В. у. решается методом Фурье, методом конечных разностей и методом преобразования Лапласа.