|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВОГНУТЫЙ И ВЫПУКЛЫЙ ОПЕРАТОРЫЗначение ВОГНУТЫЙ И ВЫПУКЛЫЙ ОПЕРАТОРЫ в математической энциклопедии: нелинейные операторы в полуупорядоченных пространствах, являющиеся аналогами вогнутых и выпуклых функций действительного переменного. Нелинейный оператор А, положительный на конусе Кв банаховом пространстве, наз. вогнутым (точнее, u0 - вогнутым на К), если: 1) для каждого ненулевого где справедливы соотношения где Аналогично, оператор А паз. выпуклым (точнее, и 0 -выпуклым на К), если выполнены условия 1) и 2), но неравенство (*) заменено противоположным, и функция Типичным примером является интегральный оператор Урысона вогнутость и выпуклость к-рого обеспечивается соответственно вогнутостью и выпуклостью скалярной функции Лит.:[1] Красносельский М. А., Геометрические методы нелинейного анализа, М., 1975. М. И. Войцеховский. |
|
|
|

 выполнены неравенства
выполнены неравенства 
 - нек-рый фиксированный ненулевой элемент из
- нек-рый фиксированный ненулевой элемент из  - положительные скалярные функции; 2) для каждого такого
- положительные скалярные функции; 2) для каждого такого  что
что 


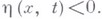

 по переменному и. Вогнутость оператора означает, что он содержит лишь "слабые" нелинейности - значения оператора на элементах конуса растут "медленно" при росте норм элементов. Выпуклость же оператора означает, как правило, что он содержит "сильные" нелинейности. В соответствии с этим уравнения с вогнутыми операторами и уравнения с выпуклыми операторами обладают рядом различий; так, первые близки по своим свойствам к соответствующим скалярным уравнениям, для вторых же такой близости нет: напр., для них, как правило, неверна теорема о единственности положительного решения.
по переменному и. Вогнутость оператора означает, что он содержит лишь "слабые" нелинейности - значения оператора на элементах конуса растут "медленно" при росте норм элементов. Выпуклость же оператора означает, как правило, что он содержит "сильные" нелинейности. В соответствии с этим уравнения с вогнутыми операторами и уравнения с выпуклыми операторами обладают рядом различий; так, первые близки по своим свойствам к соответствующим скалярным уравнениям, для вторых же такой близости нет: напр., для них, как правило, неверна теорема о единственности положительного решения.