|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВНУТРЕННИХ ВАРИАЦИЙ МЕТОДЗначение ВНУТРЕННИХ ВАРИАЦИЙ МЕТОД в математической энциклопедии: - метод в теории функций комплексного переменного, используемый при решении экстремальных задач на классах однолистных и многолистных аналитич. функций. Преимущества В. в. м. связаны с тем, что при выводе лежащих в его основе вариационных формул не делается предположений о поведении варьируемых функций на границе области Dих задания, а сами вариационные формулы являются следствием единообразного изменения функций класса на внутренних подмножествах из D. Для однолистных функций в круге В применении к классу Sфункций f(z)=z+c2z2... голоморфных и однолистных в Е, ими была установлена основная вариационная формула: в круге Характерной чертой В. в. м. является возможность, исходя из вариационных формул, получить для граничних или экстремальных функций дифференциальное уравнение. Его исследование с использованием ана-литнч. теории дифференциальных уравнений приводит к важным качественным результатам, а в ряде случаев -к полному решению экстремальной проблемы. В. в. м. нашел успешное применение в задачах о неналегающих областях; он стал составной частью так наз. вариационно-параметрического метода (см. [3]). Лит.:[1] Sсhiffer М., "Amer J. Math.", 1943, v. 65, J* 2, p. 341 -80; [2] Гол узин Г. М., "Матем. сб.", 1946, т. 19 (61), в. 2, с. 203-36; [3] его же, Геометрическая теория функций комплексного переменного, 2 изд., М., 1966. И. А. Александров. |
|
|
|

 В. в. м. был предложен М. Шиффером [1] и, в более усовершенствованной и развитой форме, Г. М. Голузиным [2].
В. в. м. был предложен М. Шиффером [1] и, в более усовершенствованной и развитой форме, Г. М. Голузиным [2].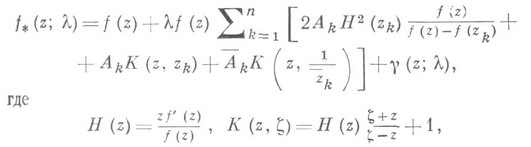
 - фиксированные точки
- фиксированные точки  - произвольные комплексные постоянные, а
- произвольные комплексные постоянные, а  при
при  стремится к нулю равно-иерно относительно z внутри Е. Иными словами, в классе S, не образующем к.-л. линейного пространства, для каждой функции
стремится к нулю равно-иерно относительно z внутри Е. Иными словами, в классе S, не образующем к.-л. линейного пространства, для каждой функции  указывается однопараметрическое семейство
указывается однопараметрическое семейство  функций этого же класса такое, что на любом замкнутом множестве в Еразложение
функций этого же класса такое, что на любом замкнутом множестве в Еразложение  по степеням
по степеням  дается записанной выше формулой. Аналогичные формулы (с оценкой порядка малости остаточного члена внутри соответствующей области) имеют место и для других классов аналитич. функций.
дается записанной выше формулой. Аналогичные формулы (с оценкой порядка малости остаточного члена внутри соответствующей области) имеют место и для других классов аналитич. функций.