"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВНУТРЕННИЙ ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОРЗначение ВНУТРЕННИЙ ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР в математической энциклопедии:
относительно поверхности  - дифференциальный оператор L(u), обладающий тем свойством, что для любой функции, для к-рой он определен, его значение в точке - дифференциальный оператор L(u), обладающий тем свойством, что для любой функции, для к-рой он определен, его значение в точке 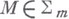 может быть вычислено лишь по значениям этой функции на ы адкой поверхности может быть вычислено лишь по значениям этой функции на ы адкой поверхности 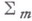 , заданной в пространстве , заданной в пространстве  В. д. о. может быть вычислен с помощью производных в направлениях l, к-рые лежат в касательном к поверхности В. д. о. может быть вычислен с помощью производных в направлениях l, к-рые лежат в касательном к поверхности  многообразии. Если ввести такие координаты, что на многообразии. Если ввести такие координаты, что на  : :
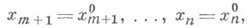
то оператор  , если он внутренний относительно , если он внутренний относительно  , после надлежащих преобразований не будет содержать производных по переменным , после надлежащих преобразований не будет содержать производных по переменным  (так наз. выводящих производных). Напр., оператор (так наз. выводящих производных). Напр., оператор
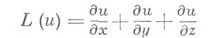
есть В. д. о. относительно любой гладкой поверхности, составленной из прямых  а также относительно любой из этих прямых. Если оператор а также относительно любой из этих прямых. Если оператор 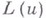 является В. д. о. относительно поверхности является В. д. о. относительно поверхности  то то 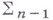 наз. характеристикой дифференциального уравнения наз. характеристикой дифференциального уравнения 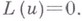
Иногда оператор наз. внутренним по отношению к поверхности  если в точках этой поверхности старший порядок выводящих производных ниже порядка оператора. Б. Л. Рождественский. если в точках этой поверхности старший порядок выводящих производных ниже порядка оператора. Б. Л. Рождественский.
|

 - дифференциальный оператор L(u), обладающий тем свойством, что для любой функции, для к-рой он определен, его значение в точке
- дифференциальный оператор L(u), обладающий тем свойством, что для любой функции, для к-рой он определен, его значение в точке 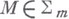 может быть вычислено лишь по значениям этой функции на ы адкой поверхности
может быть вычислено лишь по значениям этой функции на ы адкой поверхности 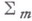 , заданной в пространстве
, заданной в пространстве  В. д. о. может быть вычислен с помощью производных в направлениях l, к-рые лежат в касательном к поверхности
В. д. о. может быть вычислен с помощью производных в направлениях l, к-рые лежат в касательном к поверхности  многообразии. Если ввести такие координаты, что на
многообразии. Если ввести такие координаты, что на  :
: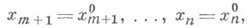
 , если он внутренний относительно
, если он внутренний относительно  , после надлежащих преобразований не будет содержать производных по переменным
, после надлежащих преобразований не будет содержать производных по переменным  (так наз. выводящих производных). Напр., оператор
(так наз. выводящих производных). Напр., оператор 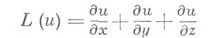
 а также относительно любой из этих прямых. Если оператор
а также относительно любой из этих прямых. Если оператор 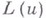 является В. д. о. относительно поверхности
является В. д. о. относительно поверхности  то
то 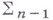 наз. характеристикой дифференциального уравнения
наз. характеристикой дифференциального уравнения 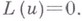
 если в точках этой поверхности старший порядок выводящих производных ниже порядка оператора. Б. Л. Рождественский.
если в точках этой поверхности старший порядок выводящих производных ниже порядка оператора. Б. Л. Рождественский.