|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЛАДИМИРОВА МЕТОДЗначение ВЛАДИМИРОВА МЕТОД в математической энциклопедии: - один из наиболее точных численных методов решения кинетич. уравнения переноса нейтронов в ядерных реакторах, основанный на интегрировании вдоль характеристик. Предложен в 1952 В.- С. Владимировым для решения интегродифференциальных кинетич. уравнений в случае сферически симметричных реакторов. Идея В. м. может быть изложена на примере задачи о расчете подкритического реактора с источником нейтронов. Для одномерной сфе- рически симметричной геометрии в односкоростном случае кинетич. уравнение для потока нейтронов
с граничным условием означающим, что на внешнюю границу приводит к уравнению где легко решается как обыкновенное дифференциальное уравнение 1-го порядка и Для каждой характеристики При этом
(где Задача на собственные значения (определение критич. параметров реактора) решается аналогично. В. м. обобщается на многоскоростные и многомерные задачи и легко программируется для ЭВМ. В отличие от Карлсона метода, В. м. использует переменную сетку по Лит.:[1] Mapчук Г. И., Методы расчета ядерных реакторов, М., 1961. в. А. Чуянов. |
|
|
|

 (где
(где  - радиус,
- радиус,  - косинус угла между вектором скорости нейтрона и радиусом) имеет вид
- косинус угла между вектором скорости нейтрона и радиусом) имеет вид

 системы снаружи
системы снаружи  нейтроны не падают, причем
нейтроны не падают, причем 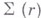 ,
,  - заданные кусочно непрерывные функции от r. Замена
- заданные кусочно непрерывные функции от r. Замена 

 . Это уравнение
. Это уравнение 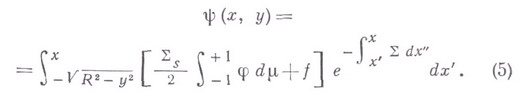
 дифференциальной части кинетич. уравнения (1) выбирается своя система узлов
дифференциальной части кинетич. уравнения (1) выбирается своя система узлов  где
где  - выбранная сетка по радиусу. Решение уравнения (5) проводится методом последовательных приближений, начиная с заданного начального приближения функции:
- выбранная сетка по радиусу. Решение уравнения (5) проводится методом последовательных приближений, начиная с заданного начального приближения функции:

 ) легко найти при помощи (5) во всех узлах сетки после того, как интегралы в (5) будут заменены суммами и будет получено выражение, связывающее значения
) легко найти при помощи (5) во всех узлах сетки после того, как интегралы в (5) будут заменены суммами и будет получено выражение, связывающее значения  и
и  в двух соседних точках на характеристике. Чтобы получить значение
в двух соседних точках на характеристике. Чтобы получить значение 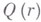 в следующем приближении, необходимо вычислить
в следующем приближении, необходимо вычислить 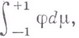 что делается с помощью квадратурной формулы, использующей точки окружности
что делается с помощью квадратурной формулы, использующей точки окружности  Скорость сходимости последовательных приближений определяется размерами и физич. характеристиками реактора.
Скорость сходимости последовательных приближений определяется размерами и физич. характеристиками реактора. для разных r, что позволяет увеличивать точность расчета на границе реактора с вакуумом (вблизи r=R) по сравнению с областями вблизи r=0, где поток нейтронов близок к изотропному.
для разных r, что позволяет увеличивать точность расчета на границе реактора с вакуумом (вблизи r=R) по сравнению с областями вблизи r=0, где поток нейтронов близок к изотропному.