|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВКЛЮЧЕНИЯ И ИСКЛЮЧЕНИЯ ПРИНЦИПЗначение ВКЛЮЧЕНИЯ И ИСКЛЮЧЕНИЯ ПРИНЦИП в математической энциклопедии: - метод подсчета числа где где Иногда метод подсчета Этот принцип , находит применение при решении комбинаторных и теоретико-числовых задач (см., напр., [1]). Так, если дано натуральное число а и Натуральные числа При помощи В. и и. п. решается также задача о беспорядках (см. [2], [3]). Лит.:[1] Холл М., Комбинаторика, пер. с англ., М., 1970; 12] Райзер Г. Дж., Комбинаторная математика, пер. с англ., М., 1966; [3] Риордан Д ж., Введение в комбинаторный анализ, пер., с англ., М., 1963. С. .4. Рукава. |
|
|
|

 объектов, не обладающих ни одним из данных свойств
объектов, не обладающих ни одним из данных свойств  по следующей формуле:
по следующей формуле:
 означает отсутствие свойства
означает отсутствие свойства  ,
,  - число всех объектов,
- число всех объектов,  - число объектов, обладающих свойством
- число объектов, обладающих свойством  - число объектов, обладающих одновременно свойствами
- число объектов, обладающих одновременно свойствами  и
и  , и т. д. (см., напр., [3]). Из В. и и. п. вытекает формула для подсчета числа объектов, обладающих точно тсвойствами из
, и т. д. (см., напр., [3]). Из В. и и. п. вытекает формула для подсчета числа объектов, обладающих точно тсвойствами из 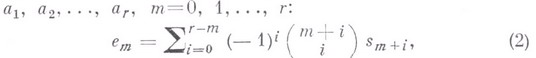
 причем здесь суммирование производится по всем k-наборам
причем здесь суммирование производится по всем k-наборам  таким, что
таким, что 
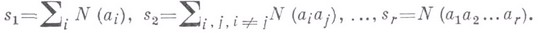
 по формуле (2) также наз. В. и и. п.
по формуле (2) также наз. В. и и. п. такие, что
такие, что  при
при  , то число целых чисел kтаких, что
, то число целых чисел kтаких, что  и не делящихся на
и не делящихся на  равно по (1):
равно по (1):