|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВИХРЬЗначение ВИХРЬ в математической энциклопедии: ротор, векторного поля где Линия в пространстве, в каждой точке к-рой в данный момент времени В. лежит на касательной прямой, наз. вихревой линией. Всякая поверхность, на к-рой расположено семейство вихревых линий, зависящее от одного параметра, наз. вихревой поверхностью. Частным, но весьма важным примером вихревых поверхностей являются вихревые трубки, к-рые образуются вихревыми линиями, выходящими из всех точек какой-нибудь замкнутой кривой. Если эта кривая бесконечно мала, то образующаяся вихревая поверхность наз. вихревой нитью. Вихревые поверхности наз. также вихревыми слоями, считая слой как бы состоящим из геометрич. поверхности с нанесенной на ней обкладкой из вихревых линий. При пересечении вихревого слоя скорости частиц жидкости испытывают тангенциальный разрыв, пропорциональный В. в соответствующей точке. Основная теорема Гельмгольца в гидродинамике заключается в том, что если объемные силы имеют потенциал, то при течении однородной, идеальной несжимаемой жидкости или баротропного газа частицы среды, расположенные в нек-рый момент времени на вихревой линии, будут и во все последующее время располагаться на вихревой линии. Таким образом, с течением времени сохраняются вихревые поверхности и, в частности, вихревые трубки и нити. Каждая вихревая трубка может быть охарактеризована нек-рым числом, наз. напряженностью трубки, и равным потоку вектора В. через произвольным образом проведенное сечение трубки. Это число не зависит от формы поперечного сечения, так как Перечисленные свойства вихревых трубок, найденные Г. Гельмгольцем (Н. Helmholtz), получают исключительно простое доказательство с помощью введенного У. Томсоном (W. Thomson) понятия о циркуляции Г скорости где ds - элемент дуги контура L. Изучение свойств циркуляции скорости приводит к теореме Лагранжа о сохранении с течением времени безвихревого движения. Основной задачей теории В. является определение поля скоростей движения жидкости по заданному полю векторов В. Если область, занятая жидкостью, безгранична во всех направлениях и если область (D), занятая В., ограничена замкнутой вихревой поверхностью, то поле скоростей находится с помощью вектор-потенциала по формуле: Если же задача состоит в определении скоростей по вихрям в ограниченном пространстве, то решение весьма сложно вследствие необходимости рассматривать интегральные уравнения с особыми ядрами. Полное решение этой задачи в [6], [7]. Для важного частного случая плоскопараллельных движений: две компоненты Лит.: 11] Aппель П., Руководство теоретической (рациональной) механики, пер. с франц., т. 3, М., 1911; [2] Вилл я Г., Теория вихрей, пер. с франц., Л.-М., 1936; [3] Liehtenstein L., Grundlagen der Hydromechanik, В., 1929; [4] Милн-Томсон Л. М., Теоретическая гидродинамика, пер. с англ., М., 1964; [5] Ламб Г., Гидродинамика, пер. с англ., М.-Л., 1947; [6] Гюнтер Н. М.. "Изв. АН СССР", 6 сер., 1926, т. 20, № 13-14, с. 1323-48; М 15-17, с. 1503 - 1532; [7] его же, "Ж. Ленингр. Физ.-матем. об-ва", 1926, т. 1, в. 1, с. 12-36. Л. Я. Сретенский. |
|
|
|

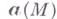 - векторная "вращательная составляющая" этого поля. Если
- векторная "вращательная составляющая" этого поля. Если 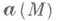 - поле скоростей частиц движущейся непрерывной среды, то В. равен половине угловой скорости частицы. В. обозначается
- поле скоростей частиц движущейся непрерывной среды, то В. равен половине угловой скорости частицы. В. обозначается 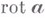 (иногда -
(иногда - 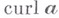 ). В декартовых прямоугольных координатах х, у, z В. определяется выражением:
). В декартовых прямоугольных координатах х, у, z В. определяется выражением: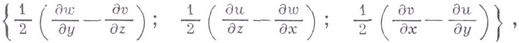
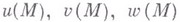 - компоненты
- компоненты 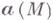 .
.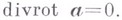 Оно означает, что вихревая трубка может быть либо замкнутой (вихревое кольцо), либо иметь начало и конец на границах жидкости. С течением времени напряженность вихревой трубки в идеальной жидкости не меняется.
Оно означает, что вихревая трубка может быть либо замкнутой (вихревое кольцо), либо иметь начало и конец на границах жидкости. С течением времени напряженность вихревой трубки в идеальной жидкости не меняется.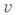 по замкнутому контуру (L).
по замкнутому контуру (L).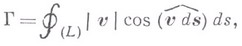

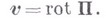

 В. равны нулю, а третья компонента
В. равны нулю, а третья компонента 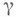 представляет собой весь В., к-рый в данном случае перпендикулярен к плоскости XOY. В пересечении вихревой нити с плоскостью XOY образуется маленькая площадка, наз. вихревой точкой. При наличии в жидкости нескольких вихревых точек возникает движение самих точек благодаря тем скоростям, какие возбуждают в жидкости эти точки. Уравнения движения вихревых точек имеют вид канонич. уравнений механики.
представляет собой весь В., к-рый в данном случае перпендикулярен к плоскости XOY. В пересечении вихревой нити с плоскостью XOY образуется маленькая площадка, наз. вихревой точкой. При наличии в жидкости нескольких вихревых точек возникает движение самих точек благодаря тем скоростям, какие возбуждают в жидкости эти точки. Уравнения движения вихревых точек имеют вид канонич. уравнений механики.