|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВИТТА ТЕОРЕМАЗначение ВИТТА ТЕОРЕМА в математической энциклопедии: всякая изометрня между двумя подпространствами F1 и F2 конечномерного векторного пространства V, определенного над полем kхарактеристики, отличной от двух, и наделенного метрич. структурой с помощью невырожденной симметрической или кососимметрической билинейной формы f, может быть продолжена до метрич. автоморфизма всего пространства V. Впервые эта теорема получена Э. Вит-том [1]. В. т. может быть доказана и в более широких предположениях на kи f (см. [2], [3]). А именно, утверждение теоремы остается в силе, если k - тело, V - левый конечномерный k-модуль, а f - невырожденная (свойство (Т)). Свойство (Т).выполняется, напр., когда f - эрмитова форма и характеристика kотлична . от двух, или когда f - знакопеременная форма. В. т. справедлива также, если k - поле, а f - симметрическая билинейная форма, ассоциированная с невырожденной квадратичной формой Q на V. Из В. т. следует, что группа метрич. автоморфизмов пространства Vтранзитивно переставляет вполне изотропные подпространства одинаковой размерности и что все максимальные вполне изотропные подпространства в Vимеют одну и ту же размерность (индекс Витта формы f). Другое следствие В. т.: классы изометрии невырожденных симметрических билинейных форм конечного ранга над kотносительно взятия ортогональной прямой суммы образуют моноид с сокращением; каноническое отображение этого моноида в его Гротендика группу инъективно. Группа WG(k) наз. группой Витта - Гротендика WG(k).поля k;тензорное произведение форм индуцирует на ней структуру кольца, к-рое наз. кольцом Витта - Гротендика поля k(см. [7]). О других приложениях В. т. см. Витта разложение, Витта кольцо. Лит.:[l] Witt Е., " J. reinc angew. Math. ", 1936, Bd 176, S. 31-44; [2] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. с франц., М., 1966; [31 Дьедонне Ж., Геометрия классических групп, пер. с франц., М., 1974; [4] Ленг С., Алгебра, пер. с англ., М., 1968; [5] Артин Э., Геометрическая алгебра, пер. с англ., М., 1969; [6] Серр Ж.-П., Курс арифметики, пер. с франц., М., 1972; [7] Милнор Д ж., "Математика", 1974, т. 15, в. 4, с. 3-27. В. Л. Попов. |
|
|
|

 -эрмитова форма (относительно нек-рого фиксированного инволютивного антиавтоморфизма
-эрмитова форма (относительно нек-рого фиксированного инволютивного антиавтоморфизма  тела k), удовлетворяющая условию: для всякого
тела k), удовлетворяющая условию: для всякого 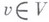 найдется такой элемент
найдется такой элемент  , что
, что