" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ВИРИАЛЬНОЕ РАЗЛОЖЕНИЕ

Значение ВИРИАЛЬНОЕ РАЗЛОЖЕНИЕ в математической энциклопедии:

внриальный ряд,- ряд в правой части уравнения состояния газа:

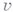где Р - давление, Т - температура, - удельный объем, k - постоянная Больцмана. Член ряда, содержащий k-й вирнальный коэффициент 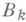, характеризует отклонение газа от идеальности, связанное с взаимодействием групп из kмолекул. 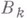выражаются через неприводимые групповые интегралы :

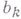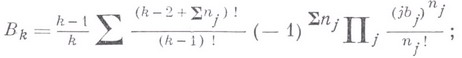
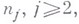суммирование идет по всем натуральным удовлетворяющим условию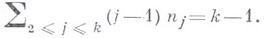

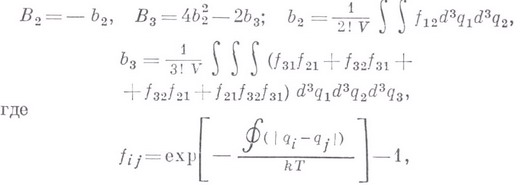
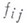В частности,

V- объем газа; интегрирование распространяется на весь объем, занятый газом. Существует правило, позволяющее с помощью записывать 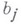для любого j. После упрощений оказывается: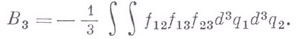

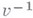Фактически удается вычислить лишь первые вириальные коэффициенты.

Рядом по степеням с коэффициентами, выраженными через 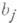, могут быть представлены s-частичные равновесные корреляционные функции, что приводит, в частности, к простому способу получения уравнения состояния (см. [3]).

Существует квантовомеханический аналог В. р.

Лит.:[1] Майер Д ж., Гепперт-Майер М., Статистическая механика, пер. с англ., М., 1952; [2] Хилл Т., Статистическая механика, пер. сангл., М., 1960; [3] Боголюбов Н. Н., Избранные труды, т. 2, Киев, 1970; [4] Уленбек Дж., Форд Д ж., Лекции по статистической механике, пер. с англ., М., 1965. И. П. Павлоцкий.