" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ВИНОГРАДОВА ТЕОРЕМА

Значение ВИНОГРАДОВА ТЕОРЕМА в математической энциклопедии:

о среднем - теорема об оценке сверху величины Виноградова интеграла:

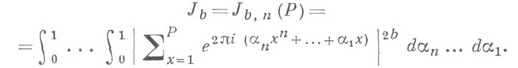
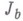- среднее значение тригонометрич. суммы. Формулируется следующим образом. Если при целом неотрицательном tположить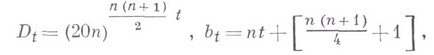

то при и целом 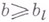будет выполняться

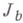Оценка , даваемая В. т., предельно точна. В. т. является основной в Виноградова методе оценок Вейля сумм. Кроме того, из нее был получен целый ряд результатов, близких к наилучшим, в классич. проблемах теории чисел (см. Варинга проблема, Гильберта - Камке проблема. Распределение дробных долей многочлена).

Лит.:[1] Виноградов И. М., Метод тригонометрических сумм в теории чисел, М., 1971; [2] Xуа Ло-ген, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964. А. А. Каращ/ба.