|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВИНОГРАДОВА ОЦЕНКИЗначение ВИНОГРАДОВА ОЦЕНКИ в математической энциклопедии: название нескольких теорем И. М. Виноградова. Наиболее известными из них являются следующие. а) В. о. сумм характеров (см. Дирихле характер). Если б) В. о. сумм Вейля (см. Вейля сумма). Пусть n - постоянное число с условием где первые слагаемые - рациональные несократимые дроби с положительными знаменателями, имеющими общим наименьшим кратным число Q, не превосходящее Точкой класса 2 наз. точка, не являющаяся точкой класса 1. Тогда, если положить то для точек класса 2 при
Если же положить то для точек класса 1 при или также в) В. о. тригонометрических сумм с простыми числами. Пусть К классу 1a отнесены точки, удовлетворяющие условиям К классу 1b отнесены точки, не являющиеся точками класса 1aи удовлетворяющие условиям Наконец, к классу 2 отнесены все остальные точки. Если положить для точек класса 1а или также для точек класса 1b, взяв (при то при Лит.:[1] Виноградов И. М., Метод тригонометрических сумм в теории чисел, М., 1971; [2] Xуа Лo-гeн. Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964. А. А. Карацуба. |
|
|
|

 - неглавный характер
- неглавный характер  , то при
, то при 

 и пусть
и пусть 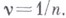 Пусть далее точки n-мерного пространства разбиты на два класса - точки класса 1 и точки класса 2. Т о ч-кой класса 1 наз. точка
Пусть далее точки n-мерного пространства разбиты на два класса - точки класса 1 и точки класса 2. Т о ч-кой класса 1 наз. точка 
 , а вторые слагаемые удовлетворяют условию
, а вторые слагаемые удовлетворяют условию 

 будет выполняться
будет выполняться 

 будет выполняться
будет выполняться 

 И пусть, в обозначениях теоремы б), точки n-мерного пространства разбиты на классы следующим образом.
И пусть, в обозначениях теоремы б), точки n-мерного пространства разбиты на классы следующим образом.

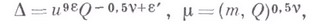

 положить
положить 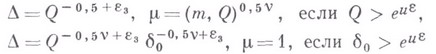
 можно брать любую из указанных пар значений
можно брать любую из указанных пар значений  и
и  ); и, наконец, для точек класса 2 положить
); и, наконец, для точек класса 2 положить 
 всегда будет выполняться
всегда будет выполняться 