|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВИНЕРОВСКИЙ ПРОЦЕССЗначение ВИНЕРОВСКИЙ ПРОЦЕСС в математической энциклопедии: однородный гауссов-ский процесс X(t) с независимыми приращениями. В. п. служит одной из математич. моделей для процесса броуновского движения. Простым преобразованием В. п. может быть превращен в "стандартный" В. п. при таких средних значениях и дисперсиях приращений это единственный непрерывный с вероятностью 1 процесс с независимыми приращениями. Ниже под В. п. будет пониматься именно этот процесс. В. п. В. п. где переходная плотность
и описывается формулой
Переходная функция где Г - уобозначает множество В. п. является непрерывным аналогом случайного блуждания частицы, к-рая в дискретные моменты времени
- случайная траектория движения такой частицы на отрезке [0, 1] (здесь Как функция со значениями в гильбертовом пространстве .
В. п. где - собственные функции оператора В, определенного формулой:
в гильбертовом пространстве Для почти всех траекторий В. п, имеют место следующие соотношения: - закон повторного логарифма; что характеризует модуль непрерывности на отрезке В применении к В. п. вида
закон повторного логарифма записывается в форме: Характер смещения броуновской частицы за конечное время tможет быть описан с помощью распределения вероятностей максимума
а отдельно взятая точка с плотностью вероятности Из приведенных выше формул легко выводятся следующие характерные свойства В. п. Броуновская траектория является нигде не дифференцируемой, причем при выходе из к.-л. точки хэта траектория за сколь угодно малое время Для В. п. как марковского однородного процесса существует инвариантная мера к-рая в силу упомянутого выше свойства инвариантности переходной функции для любых ограниченных борелевских множеств Аналогом В. п. Лит.:[1] Ито К., Маккий Г., Диффузионные процессы и их траектории, пер. с англ., М., 1968; [2] Прохоров Ю. В., Розанов Ю. А., Теория вероятностей, 2 изд., М., 1973; [3] Levy P., Prossesus stochastiques et mouve'ment brownien, 2 ed., P., 1965; [4] Павлов В. П., Броуновское движение, в кн.: БСЭ, 3 изд., т. 4. Ю. А. Розанов, |
|
|
|

 ,
,  , для к-рого
, для к-рого 
 определяется также как гаус-совский случайный процесс с нулевым математич. ожиданием и корреляционной функцией
определяется также как гаус-совский случайный процесс с нулевым математич. ожиданием и корреляционной функцией 
 может быть определен как однородный марковский процесс с переходной функцией
может быть определен как однородный марковский процесс с переходной функцией 
 есть фундаментальное решение параболического дифференциального уравнения
есть фундаментальное решение параболического дифференциального уравнения

 инвариантна относительно преобразований сдвига в фазовом пространстве:
инвариантна относительно преобразований сдвига в фазовом пространстве:

 (кратные
(кратные  ) в результате случайного воздействия каждый раз независимо от предшествующих обстоятельств смещается на величину
) в результате случайного воздействия каждый раз независимо от предшествующих обстоятельств смещается на величину 
 точнее, если при
точнее, если при 

 - целая часть nt,
- целая часть nt,  при
при  ), а
), а  - соответствующее распределение вероятностей в пространстве непрерывных функций
- соответствующее распределение вероятностей в пространстве непрерывных функций  то распределение вероятностей
то распределение вероятностей  траектории В. п.
траектории В. п.  является предельным (в смысле слабой сходимости) для распределений
является предельным (в смысле слабой сходимости) для распределений 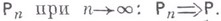
 всех случайных величин
всех случайных величин  в к-ром скалярное произведение определено формулой
в к-ром скалярное произведение определено формулой
 допускает следующее каноническое представление:
допускает следующее каноническое представление:
 - независимые гауссовские величины:
- независимые гауссовские величины:

 всех интегрируемых с квадратом (относительно лебеговской меры) функций
всех интегрируемых с квадратом (относительно лебеговской меры) функций  на отрезке [0, 1].
на отрезке [0, 1].

 ;
;


 :
:
 фиксировано,
фиксировано, а также с помощью распределения времени т первого достижения броуновской частицей фиксированной точки
а также с помощью распределения времени т первого достижения броуновской частицей фиксированной точки 

 фиксировано,
фиксировано,  (закономерности В. п. остаются без изменения при преобразовании фазового пространства
(закономерности В. п. остаются без изменения при преобразовании фазового пространства  ). Совместное распределение точки максимума
). Совместное распределение точки максимума  и самого максимума шах
и самого максимума шах  имеет плотность вероятности
имеет плотность вероятности 

 (с вероятностью 1 имеется лишь один максимум на отрезке
(с вероятностью 1 имеется лишь один максимум на отрезке  ) распределена по арксинуса закону.
) распределена по арксинуса закону.

 с вероятностью 1 бесконечно много раз пересекает "уровень" х(возвращаясь в исходную точку); с течением времени tброуновская траектория обходит все точки х, точнее
с вероятностью 1 бесконечно много раз пересекает "уровень" х(возвращаясь в исходную точку); с течением времени tброуновская траектория обходит все точки х, точнее  , с вероятностью 1 (при этом вероятное значение
, с вероятностью 1 (при этом вероятное значение  для больших химеет порядок x2); рассматриваемая на фиксированном отрезке [0, t], эта траектория имеет тенденцию достигать экстремальных значений вблизи концевых точек s=0 и s=t.
для больших химеет порядок x2); рассматриваемая на фиксированном отрезке [0, t], эта траектория имеет тенденцию достигать экстремальных значений вблизи концевых точек s=0 и s=t. :
:
 совпадает с лебеговской мерой на прямой:
совпадает с лебеговской мерой на прямой:  Время
Время  , проведенное броуновской частицей в множестве Аза промежуток от 0 до Т, таково, что с вероятностью 1
, проведенное броуновской частицей в множестве Аза промежуток от 0 до Т, таково, что с вероятностью 1
 .
. для векторного параметра
для векторного параметра  являются случайные поля, введенные П. Леви (P. Levy, см. [31).
являются случайные поля, введенные П. Леви (P. Levy, см. [31).