|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВИНЕРА ТАУБЕРОВА ТЕОРЕМАЗначение ВИНЕРА ТАУБЕРОВА ТЕОРЕМА в математической энциклопедии: если Эта теорема основана на регулярности групповой алгебры коммутативной локально компактной группы и на возможности спектрального синтеза в групповых алгебрах для замкнутых идеалов, принадлежащих лишь конечному числу регулярных максимальных идеалов [3]. Лит.:[1] Wiener N.. "Ann. Math.", 1932, v. 33, p. 1 - 100; [2] Наймарк М. А., Нормированные кольца, 2 изд., М., 1968; [3] Бур баки Н., Спектральная теория, пер. с франц., М., 1972. А. И. Штерн. |
|
|
|

 и преобразование Фурье функции
и преобразование Фурье функции 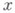 не обращается в нуль, а
не обращается в нуль, а  - функция из
- функция из 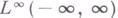 такая, что свертка
такая, что свертка  стремится к нулю при
стремится к нулю при  , то для любой
, то для любой  свертка
свертка 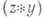 стремится к нулю при
стремится к нулю при  . Установлена Н. Винером [1]. Эта теорема обобщена на случай любой коммутативной локально компактной некомпактной группы G: если х - суммируемая относительно Хаара меры функция на Gи преобразование Фурье функции хне обращается в нуль на группе характеров
. Установлена Н. Винером [1]. Эта теорема обобщена на случай любой коммутативной локально компактной некомпактной группы G: если х - суммируемая относительно Хаара меры функция на Gи преобразование Фурье функции хне обращается в нуль на группе характеров 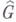 группы
группы  , а функция упринадлежит пространству
, а функция упринадлежит пространству 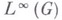 и свертка
и свертка 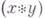 стремится к нулю на бесконечности на G, то свертка
стремится к нулю на бесконечности на G, то свертка 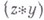 стремится к нулю на бесконечности на G для всех суммируемых функций на G.
стремится к нулю на бесконечности на G для всех суммируемых функций на G.