"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЕТВЛЕНИЯ ТОЧКАЗначение ВЕТВЛЕНИЯ ТОЧКА в математической энциклопедии:
минимальной поверхности- особая точка минимальной поверхности, в к-рой первая квадратичная форма поверхности обращается в нуль; тем самым фактически В. т. возможна лишь на обобщенной минимальной поверхности. Своим названием эта особая точка обязана тому факту, что в ее окрестности строение обобщенной минимальной поверхности подобно строению римановой поверхности функции  над точкой над точкой  , т. е. там обобщенная минимальная поверхность имеет мно-голистную ортогональную проекцию на нек-рую плоскую область, в к-рой проекция самой В. т. является внутренней точкой с единственным прообразом. В окрестности В. т. , т. е. там обобщенная минимальная поверхность имеет мно-голистную ортогональную проекцию на нек-рую плоскую область, в к-рой проекция самой В. т. является внутренней точкой с единственным прообразом. В окрестности В. т. 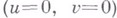 координаты координаты  минимальной поверхности представимы в виде минимальной поверхности представимы в виде
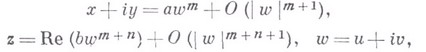
где  - две комплексные постоянные, - две комплексные постоянные, и и  - целые числа, соответственно называемые порядком и индексом В. т., ии v - внутренние изотермич. координаты. - целые числа, соответственно называемые порядком и индексом В. т., ии v - внутренние изотермич. координаты.
На основании этого представления получена теорема: если числа  - взаимно простые, то минимальная поверхность имеет - взаимно простые, то минимальная поверхность имеет  различных линий самопересечения, исходящих из В. т. с определенными направлениями, причем все соседние направления образуют между собой равные углы. различных линий самопересечения, исходящих из В. т. с определенными направлениями, причем все соседние направления образуют между собой равные углы.
Различают два вида В. т.- фальшивые В. т. и истинные (-нефальшивые). Фальшивые В. т. представляют собой особенность отображения, определяющего поверхность, и от нее можно избавиться перепараметризацией (напр., если  - регулярная минимальная поверхность, то обобщенная минимальная поверхность - регулярная минимальная поверхность, то обобщенная минимальная поверхность  будет иметь в точке будет иметь в точке  фальшивую В. т.). Истинная В. т. представляет собой реальную особенность самой поверхности, и у нее есть следующее важное свойство: в окрестности истинной В. т. поверхность можно изменить так, что новая поверхность, совпадая с исходной вне деформированной окрестности, будет иметь меньшую площадь по сравнению с исходной поверхностью. Теория обобщенных минимальных поверхностей с В. т. послужила основой для общей теории вложений с ветвлениями, развитой для широкого класса двумерных поверхностей в фальшивую В. т.). Истинная В. т. представляет собой реальную особенность самой поверхности, и у нее есть следующее важное свойство: в окрестности истинной В. т. поверхность можно изменить так, что новая поверхность, совпадая с исходной вне деформированной окрестности, будет иметь меньшую площадь по сравнению с исходной поверхностью. Теория обобщенных минимальных поверхностей с В. т. послужила основой для общей теории вложений с ветвлениями, развитой для широкого класса двумерных поверхностей в  И. X Сабитов. И. X Сабитов.
|

 над точкой
над точкой  , т. е. там обобщенная минимальная поверхность имеет мно-голистную ортогональную проекцию на нек-рую плоскую область, в к-рой проекция самой В. т. является внутренней точкой с единственным прообразом. В окрестности В. т.
, т. е. там обобщенная минимальная поверхность имеет мно-голистную ортогональную проекцию на нек-рую плоскую область, в к-рой проекция самой В. т. является внутренней точкой с единственным прообразом. В окрестности В. т. 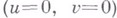 координаты
координаты  минимальной поверхности представимы в виде
минимальной поверхности представимы в виде 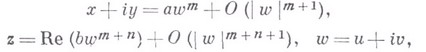
 - две комплексные постоянные,
- две комплексные постоянные, и
и  - целые числа, соответственно называемые порядком и индексом В. т., ии v - внутренние изотермич. координаты.
- целые числа, соответственно называемые порядком и индексом В. т., ии v - внутренние изотермич. координаты. - взаимно простые, то минимальная поверхность имеет
- взаимно простые, то минимальная поверхность имеет  различных линий самопересечения, исходящих из В. т. с определенными направлениями, причем все соседние направления образуют между собой равные углы.
различных линий самопересечения, исходящих из В. т. с определенными направлениями, причем все соседние направления образуют между собой равные углы. - регулярная минимальная поверхность, то обобщенная минимальная поверхность
- регулярная минимальная поверхность, то обобщенная минимальная поверхность  будет иметь в точке
будет иметь в точке  фальшивую В. т.). Истинная В. т. представляет собой реальную особенность самой поверхности, и у нее есть следующее важное свойство: в окрестности истинной В. т. поверхность можно изменить так, что новая поверхность, совпадая с исходной вне деформированной окрестности, будет иметь меньшую площадь по сравнению с исходной поверхностью. Теория обобщенных минимальных поверхностей с В. т. послужила основой для общей теории вложений с ветвлениями, развитой для широкого класса двумерных поверхностей в
фальшивую В. т.). Истинная В. т. представляет собой реальную особенность самой поверхности, и у нее есть следующее важное свойство: в окрестности истинной В. т. поверхность можно изменить так, что новая поверхность, совпадая с исходной вне деформированной окрестности, будет иметь меньшую площадь по сравнению с исходной поверхностью. Теория обобщенных минимальных поверхностей с В. т. послужила основой для общей теории вложений с ветвлениями, развитой для широкого класса двумерных поверхностей в  И. X Сабитов.
И. X Сабитов.